一.神经网络压缩
在如今人工智能的浪潮之下,深度学习在不少领域都取得了不错的成果。但是目前在边缘计算,物联网设备上的算力相比于我们的台式计算机还不太充足,我们在计算机上用于拟合的神经网络参数过多,不太适合运行在算力较弱的设备上,比如无人机,手机,平板电脑,自动驾驶汽车等等。因此我们需要将在计算机上训练好的神经网络通过某种技巧将其进行压缩,减少模型的参数,这样训练好的模型就可以迅速在这些边缘计算的设备上部署,同时达到和计算机上训练模型几乎一致的效果。比如我们常用的图像分类的模型VGG,通过改良后的MobileNet,计算量减少了10倍,输出的准确度结果甚至超越了AlexNet,准确率比Google InceptionNet也只少了0.7个百分点。那么我们有什么方法进行神经网络的压缩呢?目前比较常用的则是神经网络的剪枝,知识蒸馏,以及模型优化设计者三个方法。
二.神经网络剪枝
其实我们拟合的神经网络,很多网络的参数都过于多了,有些神经元在对结果进行的预测的时候并没有什么用,甚至是具有负面的作用。因此我们需要将其“拆除”。
拆除网络当中某些参数的方法如下:
1.剪掉权重weight约等于0的weight,让两个神经元之间失去连接
2.查看某个神经元经过activation之后的输出是否接近于零,如果接近于零,则剪掉这个神经元
3.在修剪完整个网络之后,识别的准确度肯定会下降,我们这时保留之前训练好的权重,再利用训练集训练一次,更新当前神经网络的参数
4.技巧:不要在一次修建当中修建过多的参数,不然的话神经网络很难恢复到之前的准确度,总的来说修建神经网络的流程图如下所示: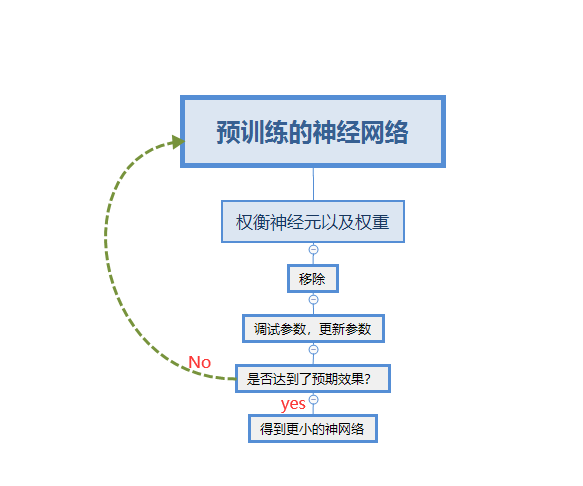
当然在有了这个更小的神经网络之后,我们就会想到为什么我们不直接去训练一个更小的神经网络呢?
原因是更小的神经网络在进行梯度下降的时候并不一定能够找到全局最小值,有可能连局部最小值都无法找到。而越大的神经网络拟合的能力就越强,就越容易在梯度下降之后找到全局最小值。
备注:但是我们在训练的时候,会遇到一些实际的问题,比如我们如果要去掉一些神经元和权重,那么我们很难用编程去实现,那我们应该怎么办呢?很简单,那就是把权重和神经网络的输出直接设置为零。这样既能够方便GPU进行加速计算,也能够方便编程实现。
三.知识蒸馏
知识蒸馏的核心就是用大的神经网络带着小的神经网络去训练。也就是我们预训练一个Teacher Net,这个模型是比较符合我们预期的。再将神经网络修剪之后得到一个Student Net,或者自定义一个Student Net,用Teacher Net带着Student Net去训练。也就是我们给Student Net和Teacher Net同样的输入,而loss则是衡量Teacher Net和student Net之间的不同。如下图所示:
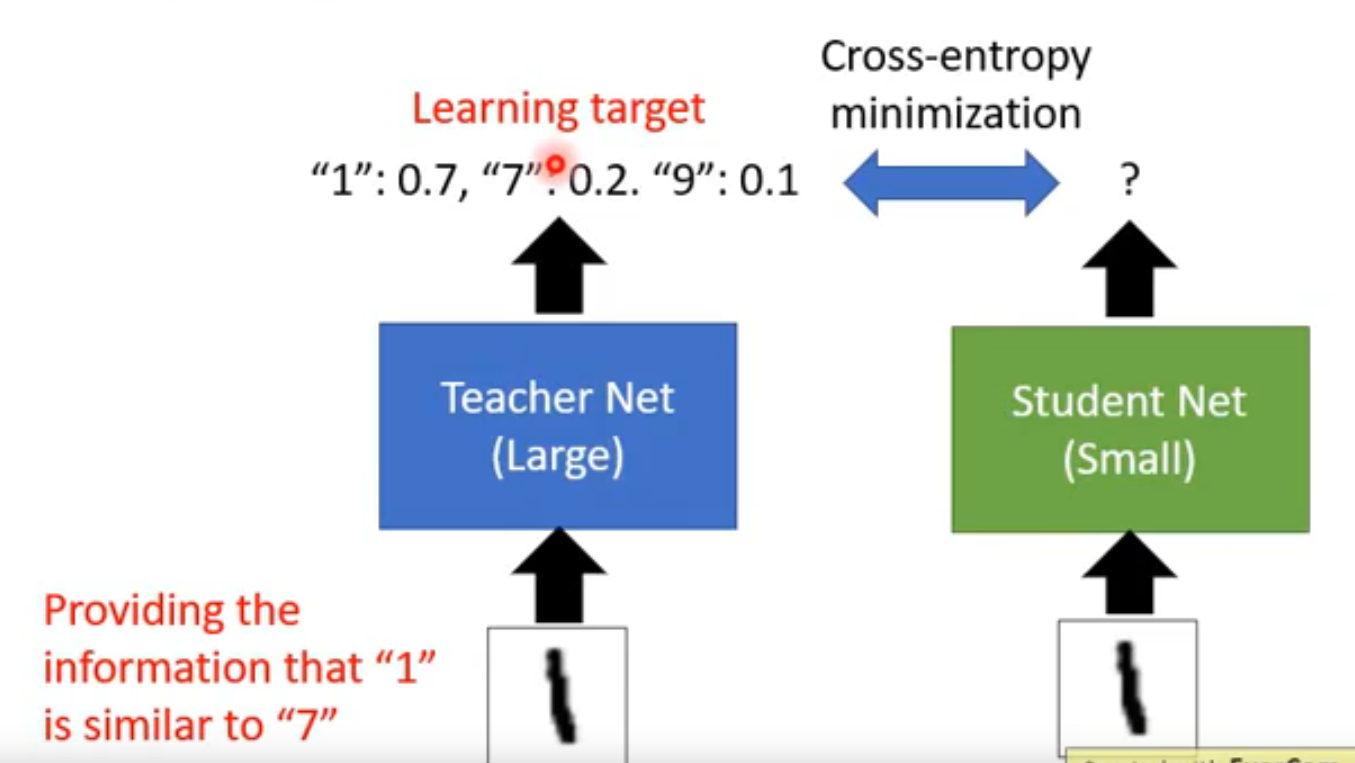
我们不用studentNet的“标签”输出来做loss,比如我们输入图像数字‘1’,神经网络输出的标签应该是“1”。不这样干,而是用Teacher Net当中的softmax输出是因为这样student-net所获得的信息更加丰富,既能够知道输出的标签应该是什么,还可以知道输出的数字是另外一个数字的相似度。假设我们输入图像1.输出的softmax的概率的值1为0.5,9为0.4,3为0.1,如果只用标签的值作为输出,studentnet绝对不知道1和9其实长得挺像的,也就差0.1的概率而已。因此这就是使用Teacher Net带着Student Net训练的好处。也是知识蒸馏当中的核心思想。
四.模型优化设计
其实在神经网络当中最常见的应该是模型的优化设计了,也是最常用对参数进行优化的方法。假设我们有一个全连接神经网络,如下图所示:
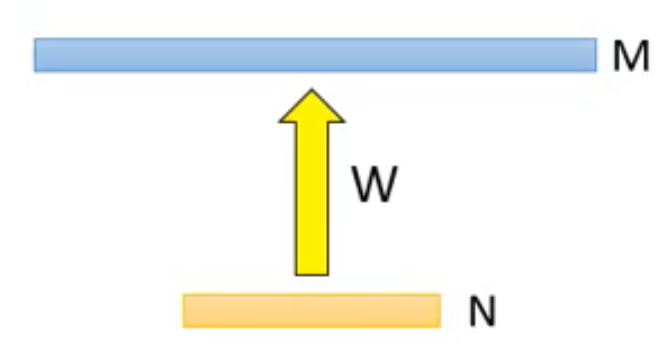
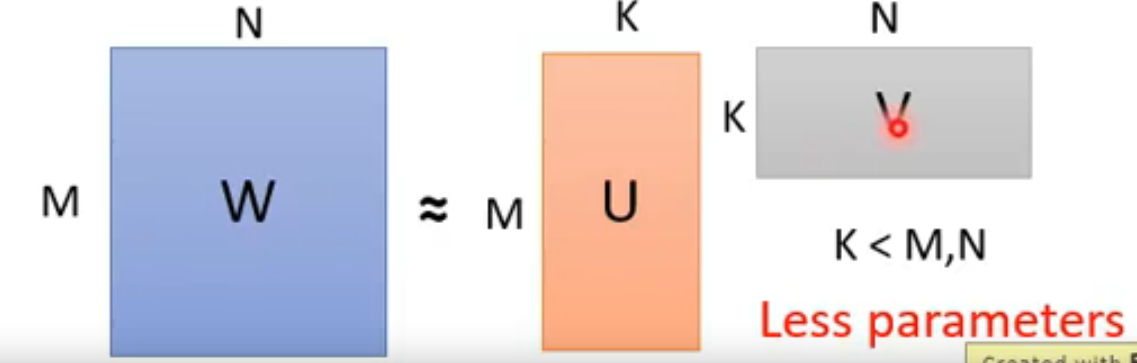
输入层具有N个神经元,输出层具有M个神经元,中间具有M*N个权重,怎么对它进行优化,减少参数呢?很简单,那就是在中间再插入一层神经元,但是这层神经元仅仅是神经元,而不具备activation,也就是激活函数。如下图所示:
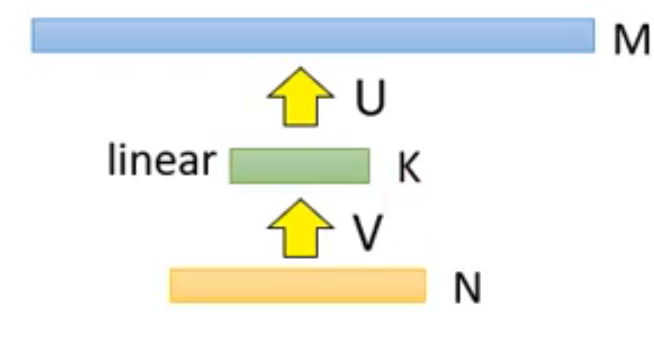
这样现在神经网络的参数总量就变成了N*K+K*M,明显小于M*N,我们下图表示权重的多少: