《剑指offer》17：二叉搜索树的后序遍历

题目描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true,否则返回false。假设输入的数组的任意两个数字都互不相同。

 

解题思路：

我们随便构造一个二叉搜索树，看看有什么规律，假设我们构造了如下图所示这样的二叉树，则有：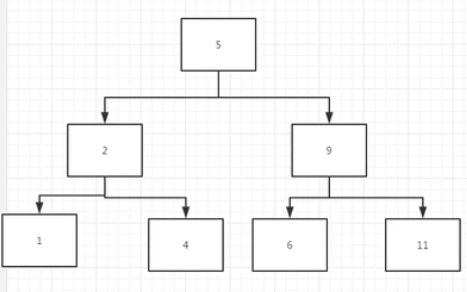

那么我们后序遍历的结果则是：[ 1,4,2,6,11,9,5]。我们可以看到最后一个数字就是这颗树的根部，同样的，由于具有二叉搜索树的特点，右边的子节点的数值一定比左边的更大，左边的数值则一定比右边的更小，因此可得[1,4,2]是我们左树遍历的结果，[6,9,11]是右树遍历的结果，我们只要在这个给定的数组当中找到了一个数值比最后一个数值更大，那么我们就找到了右子树，再用递归分别对左子树和右子树进行递归即可。因此这道题最重要的就是需要寻找到第一个需要比最后一个数字更大的那个数值的索引。代码如下：

# -*- coding:utf-8 -*-
class Solution:
    def VerifySquenceOfBST(self, sequence):
        # write code here
        if not sequence:
            return False

        root = sequence[-1]
        # 根据二叉搜索树的性质，左孩子的每个结点的值都小于根节点,这个i并不会因循环的消失而消失,i代表数组当中的索引，我们人为做的是第一次简要的递归判断
        for i in range(len(sequence)):
            if sequence[i] > root:
                break
        # 判断是否右孩子的每个结点的值都大于根结点
        for j in range(i, len(sequence)):
            if sequence[j] < root:
                return False
        left = True
        # 递归开始，i > 0 的时候证明有左孩子，i<0就证明没有。说明左树已经遍历完毕
        if i > 0:
            # 递归遍历左孩子
            left = self.VerifySquenceOfBST(sequence[ : i])
        right = True
        # 证明有右孩子，通过i的值不在最后一个结点判断，len(sequence) - 1 为sequence的最后一个结点.如果i已经在最后一个节点了，则不进行判断
        if i < len(sequence) - 1:
            right = self.VerifySquenceOfBST(sequence[i : -1])
        return left and right