hdu 6185 Covering 矩阵快速幂

题意：

用1*2和2*1的两种地毯铺地 问有多少种情况

思路：

直接推转移方程

从An-1的地方只有1种转移方法

从An-2的地方有5种转移方法

n-3转移不到n

但是n-4可以 也是最复杂的

从An-4的地方有种(An-3 - An-4)转移方法

因为n-4是从红线的地方转移过来的

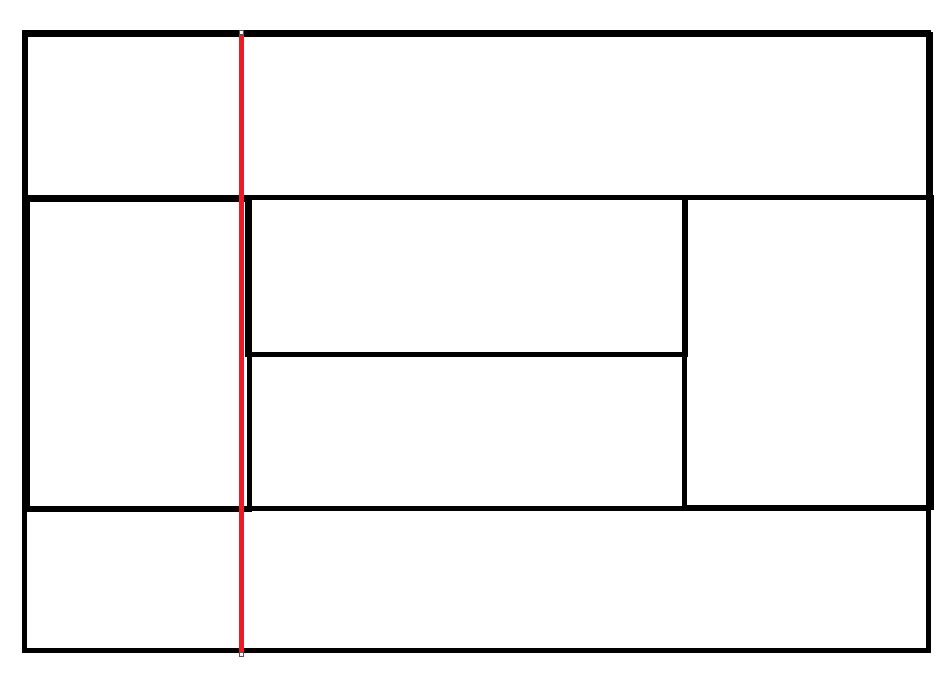
所以我们最后的转移方程就是

An = An-1 + 5*An-2 + An-3 - An-4

手推一下前4项 1 5 11 36

然后直接推矩阵写快速幂就行了

1 5 1 -1

1 0 0 0

0 1 0 0

0 0 1 0

坑点是因为有负数次幂 所以最后要+mod再%mod

最后附上快速幂模板

#include<bits/stdc++.h>
#define cl(a,b) memset(a,b,sizeof(a))
#define debug(a) cerr<<#a<<"=="<<a<<endl
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;

const int maxn=4;
const int mod=1e9+7;

struct matrix
{
    ll a[maxn][maxn];
    int row,col;
    matrix():row(maxn),col(maxn){cl(a,0);}
    matrix(int x,int y):row(x),col(y){cl(a,0);}
    void show()
    {
        for(int i=0; i<row; i++)
        {
            for(int j=0; j<col; j++)
            {
                printf("%d%c",a[i][j],j==col-1?'
':' ');
            }
        }
    }
    inline ll* operator [] (int x)
    {
        return a[x];
    }
    inline matrix operator * (matrix x)
    {
        matrix tmp(row,col);
        for (int i=0; i<row; i++)
            for (int j=0; j<col; j++)
                for (int k=0; k<row; k++)
                    tmp[i][j]=(tmp[i][j]+a[i][k]*x[k][j])%mod;
        return tmp;
    }
    inline void operator *= (matrix x)
    {
        *this = *this * x;
    }
    matrix operator ^ (ll x)
    {
        matrix result(row,col),now=*this;
        for(int i=0; i<row; i++)
        {
            result[i][i]=1;
        }
        while(x)
        {
            if(x%2) result*=now;
            now*=now;
            x/=2;
        }
        return result;
    }
};

int main()
{
    ll n,a[4]= {1,5,11,36};
    while(~scanf("%lld",&n))
    {
        if(n<=4)
        {
            printf("%lld
",a[n-1]);
        }
        else
        {
            matrix mt(4,4);
            mt[0][0]=1,mt[0][1]=5,mt[0][2]=1,mt[0][3]=-1;
            mt[1][0]=1,mt[2][1]=1,mt[3][2]=1;
            mt=mt^(n-4);
            ll ans=0;
            ans+=((36*mt[0][0]+11*mt[0][1]+5*mt[0][2]+1*mt[0][3])%mod+mod)%mod;
            printf("%lld
",ans);
        }
    }
    return 0;
}/*

1
2

*/