我们丧心病狂的教练,给我们的本期作业,竟然是
数论
这对于一个数学很渣的小蒟蒻来说,太难了啊
所以开始努力学习数论....的gcd
写这篇blog的原因——洛谷P1082
0X00 需要知道的知识
0X01 定义
gcd:若自然数d同时是自然数a和b的约数,则称d是a和b的公约数。在所有a和b的公约数中最大的一个,称为a和b的最大公约数,计为gcd(a,b)
0X02 定理
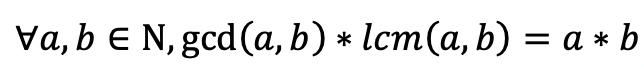
证明见lyd《算法竞赛进阶指南》0x32 最大公约数
0X03 九章算术·更相减损术
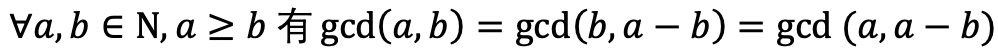
0X04 欧几里得算法

这个很有用,敲黑板划重点!!
0X10 题解
0X11 题目
题目描述
求关于xx的同余方程 ax≡1(mod b) 的最小正整数解。
输入输出格式
输入格式:
一行,包含两个正整数 a,ba,b,用一个空格隔开。
输出格式:
一个正整数 x,即最小正整数解。输入数据保证一定有解。
输入输出样例
输入样例#1:
3 10
输出样例#1:
7
0X12 重要的转化
仔细的观察一下这个方程
ax≡1(mod b)
再看看这个东西
ax+by=1(y为负整数)
哇塞他们是等价的哎
也就是说我们只需要求出一组解使等式成立就行了。且慢,再看一眼题,要求是最小的正整数解,那么只要求出最小的正整数x就完成了
怎么求呢
0X13 EXGCD
扩欧算法出现了!
void exgcd(long long a, long long b)
{
//当前目的:求解 ax + by = gcd(a, b) 这么一个方程
if(b == 0) //a, b不断改变的过程中,b最终必然会成为0
{
//在 b = 0 时等式还要成立? 使 x = 1, y = 0 ,必然成立
x = 1;
y = 0;
return;
}
exgcd(b, a % b);//把下一层系数传进去(先求下一个方程的解 )
//现在我们已经拿到了下一个方程的解x, y
long long tx = x;//暂时存一下x,别丢了
x = y;
y = tx - a / b * y;
}
这就搞定了
//
// main.cpp
// Luogu
//
// Created by gengyf on 2019/5/7.
// Copyright © 2019 yifan Geng. All rights reserved.
//
#include<cstdio>
#include<iostream>
#include<cstring>
#include<string>
//#include<bits/stdc++.h>
using namespace std;
long long a,b,x,y;
void exgcd(long xx,long yy){
if(yy==0){
x=1;y=0;return ;
}
exgcd(yy,xx%yy);
long long tx=x;
x=y;
y=tx-xx/yy*y;
}
int main(){
scanf("%lld%lld",&a,&b);
exgcd(a,b);
while(x<0){
x+=b;
x%=b;
}
printf("%lld
",x);
}