多日前的博客,放在草稿箱快发霉了,今日来填坑!!!
老早前听了一位大佬的难题选讲(难车选开)介绍了一下树链剖分,感觉很妙妙,恰好大佬降得蛮详细的,不花多少时间就理解了
在这里就来介绍一下树链剖分,巩固一下记忆。
还记得最初听一群大佬在以前难题选讲的时候,就用树链剖分来讲题,结果必然是直接全程懵逼,那时我旁边的宋爷就发誓要学这玩意儿,结果一起看博客又有点懵,没坚持下来。倒是宋爷过了一段时间继续重拾树链剖分,250+行代码强行写出,弄得我心里痒痒的,于是就学呗。。。。
【树链剖分???】
树链剖分能实现什么呢,这是我第一个想到的问题,想必初学者也疑问过,下面列举一下模板能干什么:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
操作5: 格式: x y 表示求x和y的LCA
【基础姿势】
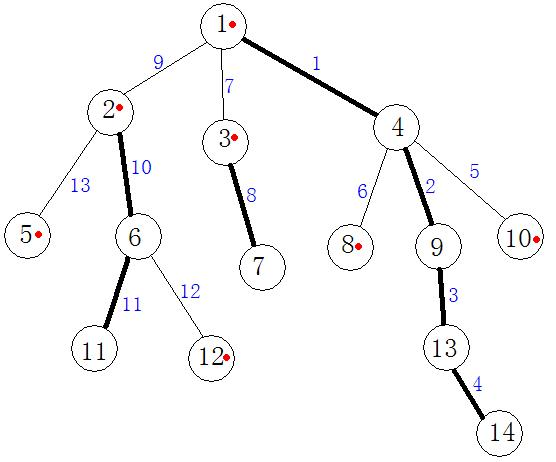
1、重儿子:每个节点的子树最大的子节点(如图中标没有红点的节点)
2、 轻儿子:除去重儿子的节点
3、重链:以每个轻儿子为起点到重儿子,路径上除起点外都是重儿子(也可以是单个轻儿子 如1—>4—>9—>13—>14)
4、轻链:除去重链以外的路径
5、链顶:每条链的起点,一定是轻儿子
6、树链剖分搜索顺序:优先深搜一个节点的重儿子,再搜其他儿子
储存结构
siz[v] 以v为根节点的子树的大小
fa[v] 节点v的父节点
son[v] 节点v的重儿子
top[v] 节点v所在链的链顶
dep[v] 节点v的深度
【建树操作】
1、dfs( )
第一次dfs我们是按dfs序来操作,更新fa[v] dep[v] siz[v] son[v]
1 int dfs(int now,int ff,int deep)
2 {
3 fa[now]=ff,dep[now]=deep,siz[now]=1;
4 int ms=-1,maxx=-1;
5 for(int i=head[now];i!=0;i=edge[i].next)
6 {
7 if(edge[i].to!=ff)
8 {
9 int gg=dfs(edge[i].to,now,deep+1);
10 if(maxx<gg)
11 { maxx=gg,ms=edge[i].to; }
12 siz[now]+=gg;
13 }
14 }
15 if(ms==-1) son[now]=now;
16 else son[now]=ms;
17 return siz[now];
18 }
1、dfs2( )
第二次dfs我们是按树链剖分的顺序来操作,更新top[v]
1 void dfs2(int now,int tt)
2 {
3 cnt++,ord[cnt]=now,idx[now]=cnt,top[now]=tt;
4 if(son[now]==now) return;
5 dfs2(son[now],tt);
6 for(int i=head[now];i!=0;i=edge[i].next)
7 {
8 if(edge[i].to!=fa[now]&&edge[i].to!=son[now])
9 dfs2(edge[i].to,edge[i].to);
10 }
11 }
接下来我们可以开始学习基本操作了(其实觉得LCA更简单,更贴切模板)
求LCA:点我查看
树链剖分模板:点我查看