2554. [福利]可持久化线段树
★★☆ 输入文件:longterm_segtree.in 输出文件:longterm_segtree.out 简单对比
时间限制:3 s 内存限制:256 MB
【题目描述】
为什么说本题是福利呢?因为这是一道非常直白的可持久化线段树的练习题,目的并不是虐人,而是指导你入门可持久化数据结构。
线段树有个非常经典的应用是处理RMQ问题,即区间最大/最小值询问问题。现在我们把这个问题可持久化一下:
Q k l r 查询数列在第k个版本时,区间[l, r]上的最大值
M k p v 把数列在第k个版本时的第p个数修改为v,并产生一个新的数列版本
最开始会给你一个数列,作为第1个版本。
每次M操作会导致产生一个新的版本。修改操作可能会很多呢,如果每次都记录一个新的数列,空间和时间上都是令人无法承受的。所以我们需要可持久化数据结构:

对于最开始的版本1,我们直接建立一颗线段树,维护区间最大值。
修改操作呢?我们发现,修改只会涉及从线段树树根到目标点上一条树链上logn个节点而已,其余的节点并不会受到影响。所以对于每次修改操作,我们可以只重建修改涉及的节点即可。就像这样:

需要查询第k个版本的最大值,那就从第k个版本的树根开始,像查询普通的线段树一样查询即可。
要计算好所需空间哦
【输入格式】
第一行两个整数N, Q。N是数列的长度,Q表示询问数
第二行N个整数,是这个数列
之后Q行,每行以0或者1开头,0表示查询操作Q,1表示修改操作M,格式为
0 k l r 查询数列在第k个版本时,区间[l, r]上的最大值 或者
1 k p v 把数列在第k个版本时的第p个数修改为v,并产生一个新的数列版本
【输出格式】
对于每个M询问,输出正确答案
【样例输入】
4 5
1 2 3 4
0 1 1 4
1 1 3 5
0 2 1 3
0 2 4 4
0 1 2 4
【样例输出】
4
5
4
4
【提示】
样例解释
序列版本1: 1 2 3 4
查询版本1的[1, 4]最大值为4
修改产生版本2: 1 2 5 4
查询版本2的[1, 3]最大值为5
查询版本1的[4, 4]最大值为4
查询版本1的[2, 4]最大值为4
数据范围
N <= 10000 Q <= 100000
对于每次询问操作的版本号k保证合法,
区间[l, r]一定满足1 <= l <= r <= N
【可持久化线段树???主席树???】
有人说可持久化线段树和主席树是一样的,又有人说,这两个不一样,不过无所谓了,反正就是实现空间的优化,同时可以查询以前的版本,大概我就知道这两个功能。每次修改的时间复杂度和增加的空间都是logn的,所以就很优越了。
那么这个优越的数据结构是如何实现的,其实我第一次看到这个高大上的算法名字时,内心是畏惧的,但后来慢慢一看一些大佬的博客,发现还是不是很难,也就是在线段树的基础上增加了一点小技巧,所以新学者不要担心,我这么蠢的都学会了,大家就不虚了。
首先我们还是来看看这张经典的可持久化线段树的图解
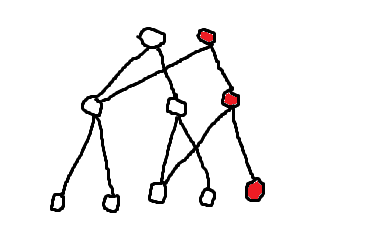
比如我们现在要修改第3个点的值,我们需要修改什么点呢,就是第3个点的所有祖先节点(图中红色节点),因为那些节点管理的区间包括第3个点(我们就不用重新建树了),当然我们更不能把这些点直接改了,因为以后可能还要查询这个版本。
所以我们就对于每个要被修改的节点,新建一个copy节点,来代替新的版本的这个节点,当然如果没有修改的节点依旧保留原来的连接方式。
然后我们就发现,如果我们要查询第k个版本的区间信息,那我们就从第k个根节点开始查询就可以了,发现是不是很简单啊,就是复制节点+从某版本根节点开始查询。
【代码实现】
1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 const int maxn=1e5+5; 5 struct sd{ 6 int l,r,maxx,son[2]; 7 }t[20*maxn+5]; 8 int root[maxn],tot,cnt; 9 void update(int v) 10 { 11 int ls=t[v].son[0],rs=t[v].son[1]; 12 t[v].maxx=max(t[ls].maxx,t[rs].maxx); 13 } 14 void build(int &v,int l,int r) 15 { 16 cnt++,v=cnt,t[v].l=l,t[v].r=r; 17 if(l==r) {scanf("%d",&t[v].maxx);return;} 18 int mid=(l+r)/2; 19 build(t[v].son[0],l,mid); 20 build(t[v].son[1],mid+1,r); 21 update(v); 22 } 23 int num; 24 void change(int v,int pos,int u) 25 { 26 if(t[v].l==t[v].r&&t[v].l==pos) 27 {t[v].maxx=u;return;} 28 int mid=(t[v].l+t[v].r)/2,ls=t[v].son[0],rs=t[v].son[1]; 29 if(pos<=mid) 30 { 31 cnt++,t[cnt]=t[ls],t[v].son[0]=cnt; 32 change(cnt,pos,u); 33 } 34 else 35 { 36 cnt++,t[cnt]=t[rs],t[v].son[1]=cnt; 37 change(cnt,pos,u); 38 } 39 update(v); 40 } 41 int ask(int v,int l,int r) 42 { 43 if(t[v].l==l&&t[v].r==r) 44 return t[v].maxx; 45 int mid=(t[v].l+t[v].r)/2,ls=t[v].son[0],rs=t[v].son[1]; 46 if(r<=mid) return ask(ls,l,r); 47 else if(l>mid) return ask(rs,l,r); 48 else return max(ask(ls,l,mid),ask(rs,mid+1,r)); 49 } 50 int main() 51 { 52 int n,m; 53 scanf("%d%d",&n,&m); 54 build(root[++tot],1,n); 55 for(int i=1;i<=m;i++) 56 { 57 int ord; 58 scanf("%d",&ord);//printf("[%d]",ord); 59 if(ord==0) 60 { 61 int k,l,r; 62 scanf("%d%d%d",&k,&l,&r); 63 printf("%d ",ask(root[k],l,r)); 64 } 65 else 66 { 67 int k,pos,u; 68 scanf("%d%d%d",&k,&pos,&u); 69 root[++tot]=++cnt;t[cnt]=t[root[k]]; 70 change(root[tot],pos,u); 71 } 72 } 73 return 0; 74 }