zoukankan      html  css  js  c++  java

  • Link Cut Tree

    想学LCT很久了，但自己看博客又没动力，前天国家队任轩笛大佬莅临讲课，虽然只是大致地带过了一下LCT，但是有了国家队大佬的BUFF就是不一样（%%%）马上来了信仰学习一波LCT。

    【什么是LCT】

    LCT即Link Cut Tree 动态树

    这个数据结构支持对树的形状进行修改，比如连边和删边。

    那么我们怎么实现呢，很显然我们需要一个可以容易改变形状的数据结构——>splay强势登场

    来张经典图，学LCT怎么能不看这张图！！！

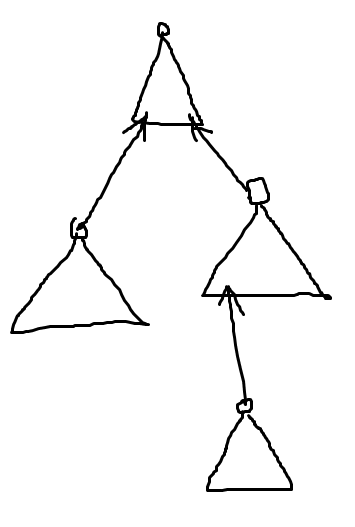
    我们的LCT就是多个splay组成的，每个splay都可以管理一条链，每条splay的根节点的父亲都不再是null了，而是另外splay的某个节点，但是当前节点记录了父亲，但是父亲并不记录这个儿子（所谓子认父不认，听起来是不是有点残忍），所以这条边就是一条虚边，而splay内部的边为实边。

    LCT的主要性质如下：

      1. 每一个Splay维护的是一条从上到下按在原树中深度严格递增的路径，且中序遍历Splay得到的每个点的深度序列严格递增。
        是不是有点抽象哈
        比如有一棵树，根节点为1（深度1），有两个儿子2,3（深度2），那么Splay有3种构成方式：
        {1−2},{3}
        {1−3},{2}
        {1},{2},{3}（每个集合表示一个Splay）
        而不能把1,2,3同放在一个Splay中（存在深度相同的点）

      2. 每个节点包含且仅包含于一个Splay中

      3. 边分为实边和虚边，实边包含在Splay中，而虚边总是由一棵Splay指向另一个节点（指向该Splay中中序遍历最靠前的点在原树中的父亲）。
        因为性质2，当某点在原树中有多个儿子时，只能向其中一个儿子拉一条实链（只认一个儿子），而其它儿子是不能在这个Splay中的。
        那么为了保持树的形状，我们要让到其它儿子的边变为虚边，由对应儿子所属的Splay的根节点的父亲指向该点，而从该点并不能直接访问该儿子（认父不认子）。

    前置知识：（其实觉得并不需要什么前置知识）但大佬们都说要先学树剖，那就学呗。

    学过树剖的人都知道，树剖是进行重链剖分，而LCT则是进行实链剖分。

    【怎么剖分？？？】

    此处应该有图了，不然就要懵逼了。。。

    如图，实线为实边，虚线为虚边。

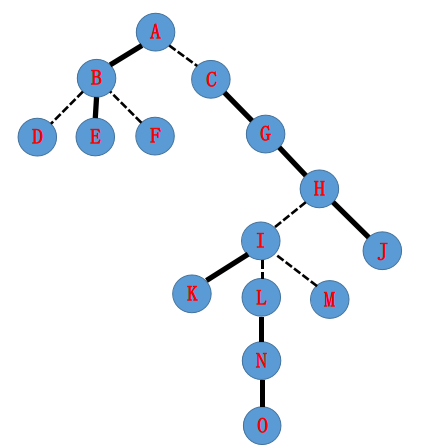
     那么我们就将由实边连成的链放在一个splay，值得注意的是实边并不固定，我们可以将其改为实边或虚边，不然怎么实现改变树的形状。

    来看看这棵树变成LCT后是什么样：（绿色方框表示一个splay）

    【LCT基本操作】

    1.access （关键操作，LCT精髓）

    这个操作j是将从某个节点到树的根节点的路径全改为实链（这里不是splay的根节点而是整棵树的）就类似于打通任督二脉一样，是不是贼帅。

    那么怎么实现呢？

    我们所要做的就是把这个节点所在splay的父节点的实链改为虚链，然后又把父节点到这个节点的虚链改为实链，但注意，首先要把这个节点的实链断掉

    我们每次先将这个点转到当前splay的根，然后把他父亲的右儿子改为当前节点，就这样一直跳到树根。

    如图所示（我们access(N)）：

    1 void access(int v)
2 {
3     for(int y=0;v;v=t[y=v].fa)
4     {
5         splay(v);
6         t[v].son[1]=y;update(v);
7     }
8 }

    2.换根操作

    我们可以把一个元素换为这棵树的根

     我们只需要一次access，再加splay就可以将这个点转到树根所在的splay的根节点，但并不是这棵树的根，因为这棵树的根在左儿子（深度最浅的点）

    但是我们会发现由于这个点是靠一个access连上去的，所以它一定是这棵splay最深的点，没错吧，所以我们只需要一次区间翻转即可将其换为根节点。

    1 void mroot(int v) 
2 {
3     access(v);
4     splay(v);
5     turn(v);//打上区间翻转标记
6 }

    掌握了上述两种基本操作后就可以通过上述两种操作进行LCT的操作了

    3.findroot 操作

    我们要找一个点所在树的树根

    首先将当前节点到根的路径打通，然后splay一路转上去，然后我们反复查左儿子就找到根了，顺便下传一下翻转标记

    1 int findroot(int v)
2 {
3     access(v),splay(v),push(v);
4     while(t[v].son[0]) v=t[v].son[0];
5     return v;
6 }

    4.split操作

    这个是来提取树上的一条链

    我们首先将节点A改为树的根节点，然后又将节点B转上去，发现树根一定就在节点B的左子树中。

    1 void split(int a,int b) {mroot(a),access(b),splay(b);}

    5.link 操作

    这里首先要看题目要求连边是不是合法

    如果一定合法，那很好我们只需要将一个节点转到树根，然后将这个节点的父节点指向另一个节点，相当于连了一条虚边

    1 void link(int a,int b) {mroot(a),t[a].fa=b;}

    如果不一定合法，那也好办，我们就判一判这两个点是不是在一棵树里，再连边

    1 void link(int a,int b) 
2 {
3     mroot(a);
4     if(findroot(b)!=a) t[a].fa=b;
5 }

    6.cut操作

    首先还是要看删边是不是合法

    如果一定合法，显然提取链之后就将splay根节点和左儿子断开就好

    1 void cut(int a,int b) 
2 {
3     split(a,b);
4     t[a].fa=t[b].son[0]=0;
5 }

    如果不一定，那就判一判

    1 void cut(int a,int b) 
2 {
3     mroot(a);
4     if(findroot(b)==a&&t[a].fa==b&&!t[a].son[1])
5     t[a].fa=t[b].son[0]=0,update(b);
6 }

    7.最后是经典的splay操作

     1 void rotate(int v)
 2 {
 3     int ff=t[v].fa,gff=t[ff].fa,which=getson(v);
 4     if(!isroot(ff)) t[gff].son[t[gff].son[1]==ff]=v;
 5     t[ff].son[which]=t[v].son[1-which],t[ff].fa=v;
 6     if(t[v].son[1-which]) t[t[v].son[1-which]].fa=ff;
 7     t[v].son[1-which]=ff,t[v].fa=gff;
 8     update(ff),update(v);//如果需要维护的话
 9 }
10 void splay(int v)
11 {
12     push(v);
13     while(!isroot(v))
14     {
15         if(!isroot(t[v].fa))
16         rotate((getson(t[v].fa)==getson(v))?t[v].fa:v);
17         rotate(v);
18     }  
19     update(v);//如果需要维护的话
20 }

    来看一道板子题

    P2147 [SDOI2008]洞穴勘测

    【代码实现】

     1 #include<cstdio>
 2 #include<iostream>
 3 using namespace std;
 4 const int maxn=10005;
 5 struct sd{
 6     int son[2],fa,rev;
 7 }t[maxn];
 8 bool getson(int v) {return t[t[v].fa].son[1]==v;}
 9 bool isroot(int v) {return t[t[v].fa].son[0]!=v&&t[t[v].fa].son[1]!=v;}
10 void update(int v)
11 {
12     if(!v) return;
13     swap(t[v].son[0],t[v].son[1]);
14     t[v].rev^=1;
15 }
16 void pushdown(int v)
17 {
18     if(t[v].rev)
19     update(t[v].son[0]),update(t[v].son[1]),t[v].rev=0;
20 }
21 void push(int v)
22 {
23     if(!isroot(v)) push(t[v].fa);
24     pushdown(v);
25 }
26 void rotate(int v)
27 {
28     int ff=t[v].fa,gff=t[ff].fa,which=getson(v);
29     if(!isroot(ff)) t[gff].son[t[gff].son[1]==ff]=v;
30     t[ff].son[which]=t[v].son[1-which],t[ff].fa=v;
31     if(t[v].son[1-which]) t[t[v].son[1-which]].fa=ff;
32     t[v].son[1-which]=ff,t[v].fa=gff;
33 }
34 void splay(int v)
35 {
36     push(v);
37     while(!isroot(v))
38     {
39         if(!isroot(t[v].fa))
40         rotate((getson(t[v].fa)==getson(v))?t[v].fa:v);
41         rotate(v);
42     }    
43 }
44 void access(int v)
45 {
46     for(int y=0;v;v=t[y=v].fa)
47     {
48         splay(v);
49         t[v].son[1]=y;
50     }
51 }
52 void mroot(int v)
53 {
54     access(v);
55     splay(v);
56     update(v);
57 }
58 void link(int a,int b) {mroot(a),t[a].fa=b;}
59 void cut(int a,int b) 
60 {
61     mroot(a),access(b),splay(b);
62     t[a].fa=t[b].son[0]=0;
63 }
64 int findroot(int v)
65 {
66     access(v),splay(v),push(v);
67     while(t[v].son[0]) v=t[v].son[0];
68     return v;
69 }
70 int main()
71 {
72     int n,m;
73     scanf("%d%d",&n,&m);
74     char ord[50];
75     for(int i=1;i<=m;i++)
76     {
77         int a,b;
78         scanf("%s%d%d",ord,&a,&b);
79         if(ord[0]=='Q') if(findroot(a)==findroot(b)) printf("Yes
");else printf("No
");
80         if(ord[0]=='C') link(a,b);
81         if(ord[0]=='D') cut(a,b);
82     }
83     return 0;
84 }
  • 相关阅读:
    Mybatis(三)
    Mybatis(二)
    Mybatis
    AJAX的跨域
    AJAX
    EL表达式与标准标签库JSTL
    java无脚本jsp页面-简介
    javaWeb的开发模式
    ADO.Net之SqlConnection、sqlcommand的应用
    翻译1-在SQL Server 2016中介绍微软R服务
  • 原文地址：https://www.cnblogs.com/genius777/p/9036812.html
Copyright © 2011-2022 走看看