什么是莫队,就是暴力嘛!!!学完后很多人都会这么说,就是有着一个很迷性质的优化,优化完了你都不知道为什么的优化。
莫队算法的效率就取决与你分块的方式了,那么我们就来看看莫队是怎样实现优化的。
先来看一道题:小B的询问
题目描述
小B有一个序列,包含N个1~K之间的整数。他一共有M个询问,每个询问给定一个区间[L..R],求Sigma(c(i)^2)的值,其中i的值从1到K,其中c(i)表示数字i在[L..R]中的重复次数。小B请你帮助他回答询问。
输入输出格式
输入格式:
第一行,三个整数N、M、K。
第二行,N个整数,表示小B的序列。
接下来的M行,每行两个整数L、R。
输出格式:
M行,每行一个整数,其中第i行的整数表示第i个询问的答案。
输入输出样例
说明
对于全部的数据,1<=N、M、K<=50000
如果你还没有学过莫队(如果学过了,还看什么博客啊!!!),这道题多半的第一反应是线段树之类的数据结构,但会发现这道题的区间合并很难实现,因为单纯质朴线段树并不资瓷某个数出现次数的合并,当然要是你写不清真的树套树(权值线段树套区间线段树)还是可以过的,说不定还贼快,但是莫队同样可以过的,我们干嘛大费周章地去写树套树呢???
首先我们来看看暴力是怎么实现的:
我们首先有两个指针,为现在处理到了的区间左端点和右端点,如果当前处理到的提问的区间的左右端点不重合,那么我们就跳跳跳!!!将指针移到需要求的区间对应左右端点,如图所示:
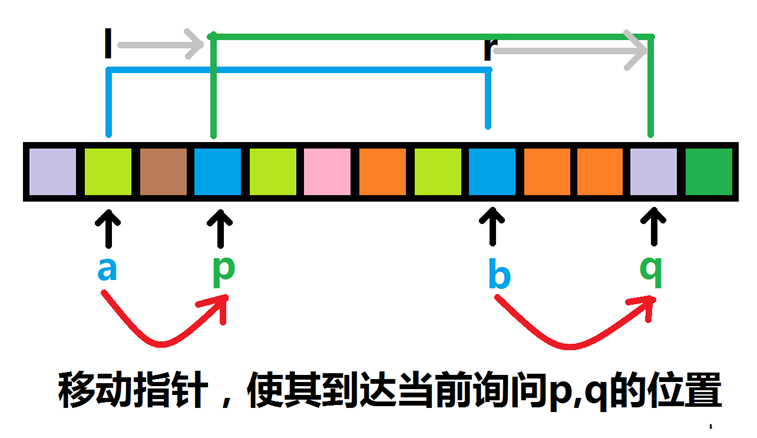
如果我们的左指针小于区间左端点,将左端点向后跳
如图,很显然我们会发现我们向右移动后,我们失去了一个黄色的块(与数字是一样的),所以黄色块的数量减一,判断一下减去这个黄色块之后,如果区间黄色块的个数变为零了,那么总的种类减一。

如果我们的右指针小于区间左端点,将右端点向后跳
如图,很显然我们会发现我们向右移动后,我们多了一个橙色的块(与数字是一样的),所以橙色块的数量加一,判断一下加上这个橙色块之后,如果区间橙色块的个数变为一了,那么总的种类加一。

左右端点的左移同理。
【莫队登场】
显然上述的暴力我们的左右指针会在区间里疯狂乱跳,跳而dying,结果肯定GG。
那么现在就需要莫队的奇妙性质来优化了,不难想到我们需要的是让指针尽量地少地跳,最好一路跳过去不用往回跳那就是O(n)的了(不过这在题目里基本不现实)。
这里发现在线的算法并不能很好地满足这样的性质,我们考虑把询问离线下来,然后对其进行排序,使其尽量优秀一点。
我们将询问的左端点进行分块操作,块的大小可以是sqrt(n)也可以是n^(2/3),但据说后者好像在带修改时最为理想。
然后我们对其排序,以左端点的所属块的顺序为第一关键字,右端点为第二关键字。
1 bool cmp(sd a,sd b) 2 { 3 if(be[a.l]==be[b.l]) return a.r<b.r; 4 return be[a.l]<be[b.l]; 5 }
当然这里排序的关键字多种多样,每道题对于不同的排序方法复杂度还不一样,所以这就是莫队很迷的地方,好像也没看到网上有统一的排序方式,只好随缘哦。。。
如果不慎,就像我一样,死在分块的道路上,TLE在黄泉路上,拉都拉不回来!!!以图为证:
莫队时间复杂度证明:(这里是借用别人的证明,看看就好)
0.首先我们知道在转移一个单位距离的时候时间复杂度是O(1)
1:对于左端点在同一块中的询问:
右端点转移的时间复杂度是O(n),一共有√n块,所以右端点转移的时间复杂度是O(n√n)
左端点每次转移最差情况是O(√n),左端点在块内会转移n次,左端点转移的时间复杂度是O(n√n);
2:对于左端点跨越块的情况:
会跨区间O(√n)次;
左端点的时间复杂度是O(√n*√n)=O(n)可以忽略不计
右端点因为在跨越块时是无序的,右端点跨越块转移一次最差可能是O(n),可能跨越块转移√n次,所以时间复杂度是O(n√n)
所以总的来说莫队的时间复杂度是O(n√n);
【代码实现】
1 #include<cstdio> 2 #include<cmath> 3 #include<cctype> 4 #include<algorithm> 5 #define N 50005 6 #define LL long long 7 using namespace std; 8 int read() 9 { 10 int c,x,f; 11 while(!isdigit(c=getchar())&&c!='-'); c=='-'?(x=0,f=1):(x=c-'0',f=0); 12 while(isdigit(c=getchar())) x=(x<<3)+(x<<1)+c-'0'; return f?-x:x; 13 } 14 int n,m,k,x[N],cnt[N]; 15 LL ANS[N]; 16 struct que{ 17 int l,r,id,b; 18 }q[N]; 19 bool cmp(que a,que b) 20 { 21 if(a.b==b.b) return a.r<b.r; 22 return a.l<b.l; 23 } 24 int main() 25 { 26 n=read(); m=read(); k=read(); 27 int size=sqrt(n); 28 for(int i=1;i<=n;i++) x[i]=read(); 29 for(int i=1;i<=m;i++) 30 q[i].l=read(),q[i].r=read(),q[i].id=i,q[i].b=(q[i].l-1)/size+1; 31 sort(q+1,q+m+1,cmp); 32 int l=1,r=0; LL ans=0; 33 for(int i=1;i<=m;i++) 34 { 35 while(l>q[i].l) l--,cnt[x[l]]++,ans+=2*cnt[x[l]]-1; 36 while(r<q[i].r) r++,cnt[x[r]]++,ans+=2*cnt[x[r]]-1; 37 while(r>q[i].r) cnt[x[r]]--,ans-=2*cnt[x[r]]+1,r--; 38 while(l<q[i].l) cnt[x[l]]--,ans-=2*cnt[x[l]]+1,l++; 39 ANS[q[i].id]=ans; 40 } 41 for(int i=1;i<=m;i++) printf("%lld ",ANS[i]); 42 return 0; 43 }