11.19 考试总结

好久没写博客了，今天更一波。

T1 seq

Desprition

游戏一开始有 (n) 个正整数，((2<=n<=262144))，范围在 (1-40) 。在一步中，贝西可以选相邻的两个相同的数，然后合并成一个比原来的大一的数（例如两个(7) 合并成一个(8))，目标是使得最大的数最大，请帮助Bessie来求最大值。

solution

洛谷原题

自闭了，考试的时候没想出来，写了个假的算法骗了点分。

考完之后发现自己做过？？？四月多做的，那没事了。

设 (f[i][j]) 表示 以 (j) 为左端点合并出 (i) 的右端点的位置，即 (j-f[i][j]-1) 这一段区间可以合成一个 (i).

转移的时候则有 (f[i][j] = f[i-1][f[i-1][j]]).

可以画个图理解一下(图上下面的两个 (i) 好像应该是 (i-1)， 但是我懒得改了)：

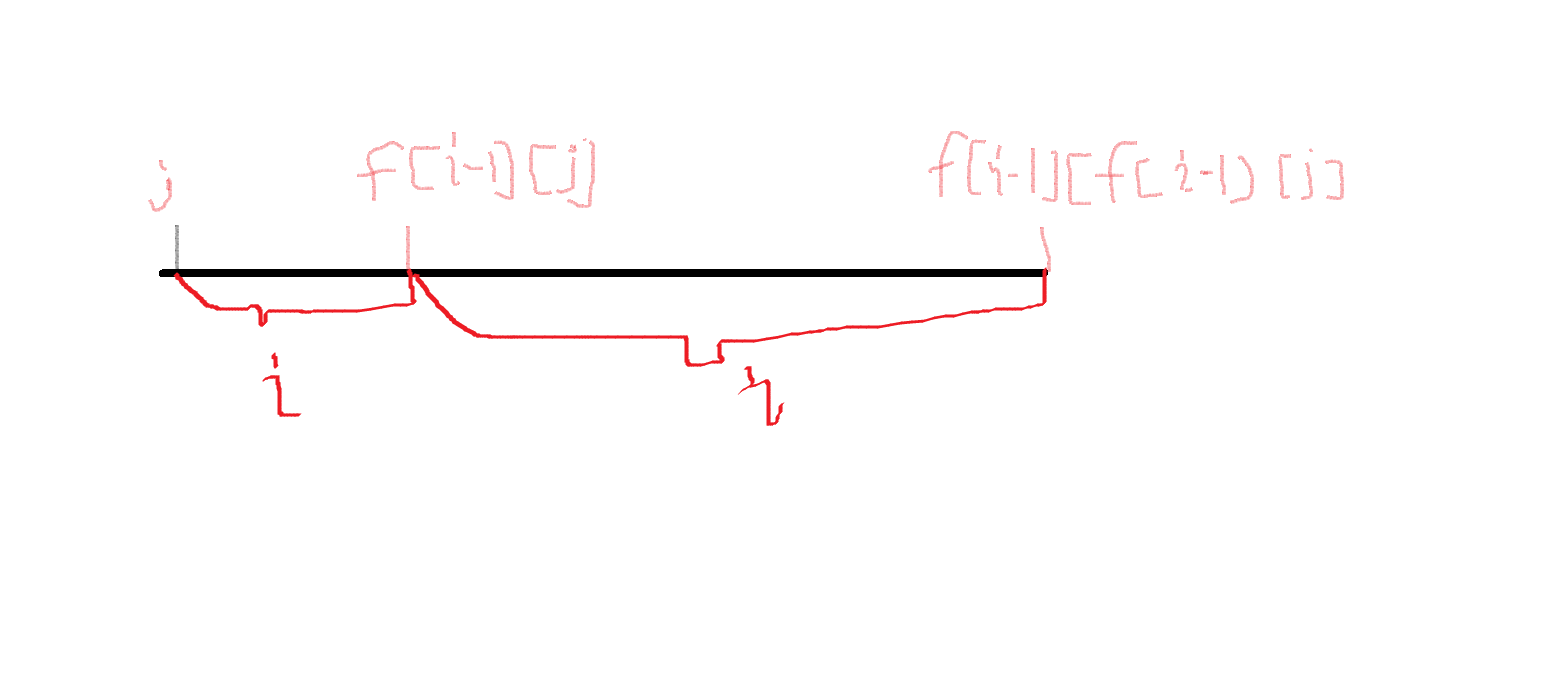
(j-f[i-1][j]-1) 合成出一个 (i-1) 来，如果 (f[i-1][j]-f[i-1][f[i-1][j]]) 也可以合并出一个 (i-1) .

那么这两个 (i-1) 就可以合并出一个 (i).

初始化 (f[a[i]][i] = i+1). 复杂度 (O(60n))

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
const int N = 3e5+10;
int n,maxn;
int a[N],f[60][265000];
inline int read()
{
	int s = 0,w = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
	return s * w;
}
int main()
{
	freopen("seq.in","r",stdin);
	freopen("seq.out","w",stdout);
	n = read();
	for(int i = 1; i <= n; i++)
	{
		a[i] = read();
		f[a[i]][i] = i + 1;
	}
	for(int i = 2; i <= 60; i++)
	{
		for(int j = 1; j <= n; j++)
		{
			if(!f[i][j]) f[i][j] = f[i-1][f[i-1][j]];
			if(f[i][j]) ans = i;
		}
	}
	printf("%d
",ans);
	fclose(stdin); fclose(stdout);
	return 0;
}

T2 sum

Desprition

(f(n)) 表示从 ([1,n-1]) 中任选两个数 (a,b) 满足 (a imes b) 不是 (n) 的倍数的方案数。 (g(n) = displaystylesum_{dmid n} f(n))

下面有 (T) 组询问，每个询问输入一个，请你给出 (g(n)) 的值。

(nleq 10^9,Tleq 10^3)

solution

机房大佬口中的反演板子题，然鹅我不会。

注：下面柿子中的 (*) 号为 卷积符号， $ imes $ 为乘号, (e) 函数为单位 1函数。

颓柿子。

(f(n) = n^2 - displaystylesum_{a=1}^{n}sum_{b=1}^{n} [a imes bmid n])

把 (a imes b) 和 (n) 同时除以一个 (gcd(a,n)) 可以变成。

(f(n) = n^2 - displaystylesum_{a=1}^{n}sum_{b=1}^{n} [{a imes bover gcd(a,n)}mid {nover gcd(a,n)}])

然后你会发现 (aover gcd(a,n)) 其实是和 (nover gcd(a,n)) 是互质的，因为他们两个的因数全部都除掉了。

然后柿子可以化为:

(f(n) = n^2 - displaystylesum_{a=1}^{n}sum_{b=1}^{n} [bmid {nover gcd(a,n)}])

他其实等价于：

(f(n) = n^2- displaystylesum_{a=1}^{n} gcd(a,n)).

这一步需要好好理解一下，后面的 (displaystylesum_{b=1}^{n} [bmid {nover gcd(a,n)}])， 其实求的是 (1-n) 这个范围内 (nover {gcd(a,n)}) 的倍数有多少个。

他就等价于 (nover {nover gcd(a,n)}) = (gcd(a,n)).

继续化简可得： (f(n) = n^2 - displaystylesum_{dmid n} {phi({nover d})} imes d)

那么 (g(n) = displaystylesum_{dmid n} sum_{pmid d} d^2 - phi({dover p}) imes p)

把 (d^2) 提出来变成 :

(g(n) = displaystylesum_{dmid n} d^2 - sum_{dmid n}sum_{pmid d}phi({dover p}) imes p)

然后你会发现后面的 (displaystylesum_{pmid d}phi({dover p}) imes p) 其实是个卷积的形式，相当于 (phi(d) * id(d))

代入可得：

(g(n) = displaystylesum_{dmid n} d^2 - sum_{dmid n} phi(d)*id(d))

设 (F(n) = phi(n)*id(n))，则 (g(n) = displaystylesum_{dmid n} d^2-sum_{dmid n} F(d))

后面你会发现不好化简了，并且 (displaystylesum_{dmid n}F(d)) 长的像个卷积的形式，所以我们在保证原式不变的情况下，加一个 (e({nover d})) 变成：

(g(n) = displaystylesum_{dmid n} d^2-sum_{dmid n} F(d) imes e({nover d}))

转化为卷积形式变成：

(g(n) = displaystylesum_{dmid n} d^2-F(n)*e(n)).

把 (F) 展开，且卷积有交换律可得：

(g(n) = displaystylesum_{dmid n} d^2-phi(n)*e(n)* id(n))

又有 (phi(n)*e(n) = id(n)) ,所以：

(g(n) = displaystylesum_{dmid n} d^2-id(n) * id(n))

把卷积拆开可得：

(g(n) = displaystylesum_{dmid n} d^2-sum_{dmid n} n imes {nover d})

所以 (g(n) = displaystylesum_{dmid n} d^2-sum_{dmid n} n)

综上可得，最后答案为 (n) 的因数的平方和减去 (n imes n的约数个数和)

直接 (O(sqrt n)) 求这可以。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
#define int long long
int T,n;
inline int read()
{
	int s = 0,w = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
	return s * w;
}
int calc(int n)
{
	int ans = 0;
	for(int i = 1; i <= sqrt(n); i++)
	{
		if(n % i == 0)
		{
			ans += i * i - n;
			if(i * i != n) ans += (n/i) * (n/i) - n;
		}
	}
	return ans;
}
signed main()
{
	freopen("sum.in","r",stdin);
	freopen("sum.out","w",stdout);
	T = read();
	while(T--)
	{
		n = read();
		printf("%lld
",calc(n));
	}
	fclose(stdin); fclose(stdout);
	return 0;
}