机器学习 | 算法笔记- K均值（K-Means）

前言

本系列为机器学习算法的总结和归纳，目的为了清晰阐述算法原理，同时附带上手代码实例，便于理解。

目录

　　k近邻（KNN）

　　决策树

　　线性回归

　　逻辑斯蒂回归

　　朴素贝叶斯

　　支持向量机（SVM）

　　组合算法（Ensemble Method）

　　K-Means

　　机器学习算法总结

 

本章主要介绍无监督学习中的k-means，以及简单代码实现。

一、算法简介

k-Means算法是一种聚类算法，它是一种无监督学习算法，目的是将相似的对象归到同一个蔟中。蔟内的对象越相似，聚类的效果就越好。聚类和分类最大的不同在于，分类的目标事先已知，而聚类则不一样。其产生的结果和分类相同，而只是类别没有预先定义。

1.1 算法原理

设计的目的：使各个样本与所在簇的质心的均值的误差平方和达到最小（这也是评价K-means算法最后聚类效果的评价标准）。

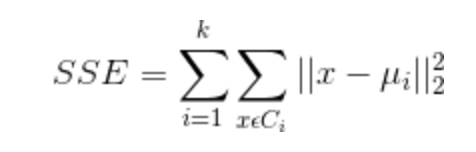
1.2 算法特点

· 优点：容易实现

· 缺点：可能收敛到局部最小值，在大规模数据上收敛较慢

适合数据类型：数值型数据

1.3 聚类过程

1）创建k个点作为k个簇的起始质心（经常随机选择）。

2）分别计算剩下的元素到k个簇中心的相异度（距离），将这些元素分别划归到相异度最低的簇。

3）根据聚类结果，重新计算k个簇各自的中心，计算方法是取簇中所有元素各自维度的算术平均值。

4）将D中全部元素按照新的中心重新聚类。

5）重复第4步，直到聚类结果不再变化。

6）最后，输出聚类结果。

二、算法实现

2.1 伪代码

1 创建k个点作为K个簇的起始质心（经常随机选择）
2 当任意一个点的蔟分配结果发生变化时（初始化为True）
3     对数据集中的每个数据点，重新分配质心
4         对每个质心
5             计算质心到数据点之间的距离
6         将数据点分配到距其最近的蔟
7     对每个蔟，计算蔟中所有点的均值并将均值作为新的质心

2.2 手写实现

代码主要包括两部分，一个是Kmeans分类器的构建，里面包含两个算法，一个是Kmeans，一个是二分K-means。另一个是一个测试文件代码，用于执行测试test.txt数据文件

# -*- coding: utf-8 -*-
import numpy as np

class KMeansClassifier():
    
    def __init__(self, k=3, initCent='random', max_iter=500 ):
        
        self._k = k
        self._initCent = initCent
        self._max_iter = max_iter
        self._clusterAssment = None
        self._labels = None
        self._sse = None
        
    def _calEDist(self, arrA, arrB):
        """
        功能：欧拉距离距离计算
        输入：两个一维数组
        """
        return np.math.sqrt(sum(np.power(arrA-arrB, 2)))
    
    def _calMDist(self, arrA, arrB):
        """
        功能：曼哈顿距离距离计算
        输入：两个一维数组
        """
        return sum(np.abs(arrA-arrB))


    def _randCent(self, data_X, k):
        """
        功能：随机选取k个质心
        输出：centroids #返回一个m*n的质心矩阵
        """
        n = data_X.shape[1] #获取特征的维数
        centroids = np.empty((k,n))  #使用numpy生成一个k*n的矩阵，用于存储质心
        for j in range(n):
            minJ = min(data_X[:, j])
            rangeJ  = float(max(data_X[:, j] - minJ))
            #使用flatten拉平嵌套列表(nested list)
            centroids[:, j] = (minJ + rangeJ * np.random.rand(k, 1)).flatten()
        return centroids 
    
    def fit(self, data_X):
        """
        输入：一个m*n维的矩阵
        """
        if not isinstance(data_X, np.ndarray) or 
               isinstance(data_X, np.matrixlib.defmatrix.matrix):
            try:
                data_X = np.asarray(data_X)
            except:
                raise TypeError("numpy.ndarray resuired for data_X")
                
        m = data_X.shape[0]  #获取样本的个数
        #一个m*2的二维矩阵，矩阵第一列存储样本点所属的族的索引值，
        #第二列存储该点与所属族的质心的平方误差
        self._clusterAssment = np.zeros((m,2)) 
        
        if self._initCent == 'random':
            self._centroids = self._randCent(data_X, self._k)
            
        clusterChanged = True
        for _ in range(self._max_iter): #使用"_"主要是因为后面没有用到这个值
            clusterChanged = False
            for i in range(m):   #将每个样本点分配到离它最近的质心所属的族
                minDist = np.inf #首先将minDist置为一个无穷大的数
                minIndex = -1    #将最近质心的下标置为-1
                for j in range(self._k): #次迭代用于寻找最近的质心
                    arrA = self._centroids[j,:]
                    arrB = data_X[i,:]
                    distJI = self._calEDist(arrA, arrB) #计算误差值
                    if distJI < minDist:
                        minDist = distJI
                        minIndex = j
                if self._clusterAssment[i, 0] != minIndex or self._clusterAssment[i, 1] > minDist**2:
                    clusterChanged = True
                    self._clusterAssment[i,:] = minIndex, minDist**2
            if not clusterChanged:#若所有样本点所属的族都不改变,则已收敛,结束迭代
                break
            for i in range(self._k):#更新质心，将每个族中的点的均值作为质心
                index_all = self._clusterAssment[:,0] #取出样本所属簇的索引值
                value = np.nonzero(index_all==i) #取出所有属于第i个簇的索引值
                ptsInClust = data_X[value[0]]    #取出属于第i个簇的所有样本点
                self._centroids[i,:] = np.mean(ptsInClust, axis=0) #计算均值
        
        self._labels = self._clusterAssment[:,0]
        self._sse = sum(self._clusterAssment[:,1])
    
    def predict(self, X):#根据聚类结果，预测新输入数据所属的族
        #类型检查
        if not isinstance(X,np.ndarray):
            try:
                X = np.asarray(X)
            except:
                raise TypeError("numpy.ndarray required for X")
        
        m = X.shape[0]#m代表样本数量
        preds = np.empty((m,))
        for i in range(m):#将每个样本点分配到离它最近的质心所属的族
            minDist = np.inf
            for j in range(self._k):
                distJI = self._calEDist(self._centroids[j,:], X[i,:])
                if distJI < minDist:
                    minDist = distJI
                    preds[i] = j
        return preds

        
class biKMeansClassifier():
    "this is a binary k-means classifier"
    
    def __init__(self, k=3):
        
        self._k = k
        self._centroids = None
        self._clusterAssment = None
        self._labels = None
        self._sse = None
        
    
    def _calEDist(self, arrA, arrB):
        """
        功能：欧拉距离距离计算
        输入：两个一维数组
        """
        return np.math.sqrt(sum(np.power(arrA-arrB, 2)))
        
    def fit(self, X):
        m = X.shape[0]
        self._clusterAssment = np.zeros((m,2))
        centroid0 = np.mean(X, axis=0).tolist()
        centList =[centroid0]
        for j in range(m):#计算每个样本点与质心之间初始的平方误差
            self._clusterAssment[j,1] = self._calEDist(np.asarray(centroid0), 
                                        X[j,:])**2
        
        while (len(centList) < self._k):
            lowestSSE = np.inf
            #尝试划分每一族,选取使得误差最小的那个族进行划分
            for i in range(len(centList)):
                index_all = self._clusterAssment[:,0] #取出样本所属簇的索引值
                value = np.nonzero(index_all==i) #取出所有属于第i个簇的索引值
                ptsInCurrCluster = X[value[0],:] #取出属于第i个簇的所有样本点
                clf = KMeansClassifier(k=2)
                clf.fit(ptsInCurrCluster)
                #划分该族后，所得到的质心、分配结果及误差矩阵
                centroidMat, splitClustAss = clf._centroids, clf._clusterAssment
                sseSplit = sum(splitClustAss[:,1])
                index_all = self._clusterAssment[:,0] 
                value = np.nonzero(index_all==i)
                sseNotSplit = sum(self._clusterAssment[value[0],1])
                if (sseSplit + sseNotSplit) < lowestSSE:
                    bestCentToSplit = i
                    bestNewCents = centroidMat
                    bestClustAss = splitClustAss.copy()
                    lowestSSE = sseSplit + sseNotSplit
            #该族被划分成两个子族后,其中一个子族的索引变为原族的索引
            #另一个子族的索引变为len(centList),然后存入centList
            bestClustAss[np.nonzero(bestClustAss[:,0]==1)[0],0]=len(centList)
            bestClustAss[np.nonzero(bestClustAss[:,0]==0)[0],0]=bestCentToSplit
            centList[bestCentToSplit] = bestNewCents[0,:].tolist()
            centList.append(bestNewCents[1,:].tolist())
            self._clusterAssment[np.nonzero(self._clusterAssment[:,0] == 
                                        bestCentToSplit)[0],:]= bestClustAss 
                   
        self._labels = self._clusterAssment[:,0] 
        self._sse = sum(self._clusterAssment[:,1])
        self._centroids = np.asarray(centList)
                                
    def predict(self, X):#根据聚类结果，预测新输入数据所属的族
        #类型检查
        if not isinstance(X,np.ndarray):
            try:
                X = np.asarray(X)
            except:
                raise TypeError("numpy.ndarray required for X")
        
        m = X.shape[0]#m代表样本数量
        preds = np.empty((m,))
        for i in range(m):#将每个样本点分配到离它最近的质心所属的族
            minDist = np.inf
            for j in range(self._k):
                distJI = self._calEDist(self._centroids[j,:],X[i,:])
                if distJI < minDist:
                    minDist = distJI
                    preds[i] = j
        return preds

View Code

# -*- coding: utf-8 -*-

import pandas as pd
import numpy as np
from kmeans import KMeansClassifier
import matplotlib.pyplot as plt

#加载数据集，DataFrame格式，最后将返回为一个matrix格式
def loadDataset(infile):
    df = pd.read_csv(infile, sep='	', header=0, dtype=str, na_filter=False)
    return np.array(df).astype(np.float)

if __name__=="__main__":
    data_X = loadDataset(r"data/testSet.txt")
    k = 3
    clf = KMeansClassifier(k)
    clf.fit(data_X)
    cents = clf._centroids
    labels = clf._labels
    sse = clf._sse
    colors = ['b','g','r','k','c','m','y','#e24fff','#524C90','#845868']
    for i in range(k):
        index = np.nonzero(labels==i)[0]
        x0 = data_X[index, 0]
        x1 = data_X[index, 1]
        y_i = i
        for j in range(len(x0)):
            plt.text(x0[j], x1[j], str(y_i), color=colors[i], 
                        fontdict={'weight': 'bold', 'size': 6})
        plt.scatter(cents[i,0],cents[i,1],marker='x',color=colors[i],
                    linewidths=7)
    
    plt.title("SSE={:.2f}".format(sse))
    plt.axis([-7,7,-7,7])
    outname = "./result/k_clusters" + str(k) + ".png"
    plt.savefig(outname)
    plt.show()
    
    

View Code

三、算法总结与讨论

虽然K-Means算法原理简单，但是也有自身的缺陷：

• 首先，聚类的簇数K值需要事先给定，但在实际中这个 K 值的选定是非常难以估计的，很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适。
• Kmeans需要人为地确定初始聚类中心，不同的初始聚类中心可能导致完全不同的聚类结果，不能保证Ｋ-Means算法收敛于全局最优解。

• 针对此问题，在K-Means的基础上提出了二分K-means算法。该算法首先将所有点看做是一个簇，然后一分为二，找到最小SSE的聚类质心。接着选择其中一个簇继续一分为二，此处哪一个簇需要根据划分后的SSE值来判断。

• 对离群点敏感。
• 结果不稳定 （受输入顺序影响）。
• 时间复杂度高O(nkt)，其中n是对象总数，k是簇数，t是迭代次数。

- K-Means算法K值如何选择？

《大数据》中提到：给定一个合适的类簇指标，比如平均半径或直径，只要我们假设的类簇的数目等于或者高于真实的类簇的数目时，该指标上升会很缓慢，而一旦试图得到少于真实数目的类簇时，该指标会急剧上升。

 

簇的直径是指簇内任意两点之间的最大距离。

簇的半径是指簇内所有点到簇中心距离的最大值。

 

- 如何优化K-Means算法搜索的时间复杂度？

可以使用K-D树来缩短最近邻的搜索时间（NN算法都可以使用K-D树来优化时间复杂度）。

 

- 如何确定K个簇的初始质心？

1) 选择批次距离尽可能远的K个点

 首先随机选择一个点作为第一个初始类簇中心点，然后选择距离该点最远的那个点作为第二个初始类簇中心点，然后再选择距离前两个点的最近距离最大的点作为第三个初始类簇的中心点，以此类推，直至选出K个初始类簇中心点。

 2) 选用层次聚类或者Canopy算法进行初始聚类，然后利用这些类簇的中心点作为KMeans算法初始类簇中心点。

 

聚类扩展：密度聚类、层次聚类。详见：

 

参考：http://www.csuldw.com/2015/06/03/2015-06-03-ml-algorithm-K-means/