1. 什么是车间调度(JobShop)问题
- Job,在车间调度中被称为工件。一个工件又由若干道工序组成。
- resource, 资源。在车间调度中一般指的是机器,每道工序需要在某个机器上加工。
- Constraint, 约束。在车间调度中约束主要有以下两种:
- 同一个工件包含的每道工序有先后顺序。
- 每个机器不能并行同时处理两道工序。
- Objective目标。车间调度问题的一个常见目标是使所有工件完成的总时间最小。
- 一个车间调度问题可以用一个已知条件表格来刻画,例如下面的已知条件表格:
| 第一个工件的第一道工序 | 第一个工件的第二道工序 | 第二个工件的第一道工序 | 第二个工件的第二道工序 | |
| 机器号 | 1 | 2 | 2 | 1 |
| 加工时间 | 3 | 2 | 5 | 1 |
以上面的问题为例,我们的目标是为每个工件的每道工序指定一个开始时间,工人师傅按照这个时间在相应机器上开始操作该道工序。上面这个车间调度问题可以用一个带权有向无环图来表示:
上面已知条件表格对应的加权有向无环图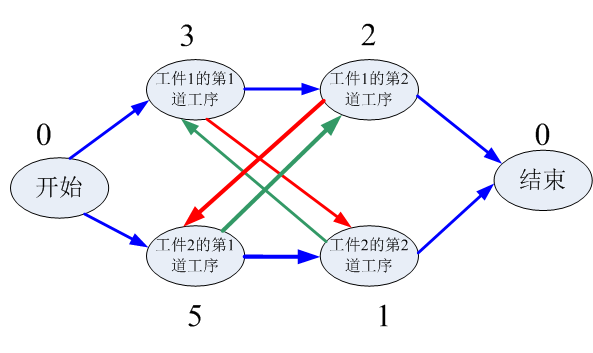
这个加权有向无环图就代表上面的表格,我们可以看到每个工序作为图中的一个节点出现,权重就是这个节点对应的加工时间。此外,我们增加两个虚拟节点,一个是开始节点,结束节点。约束条件用箭头表示,在这里需要注意的是:同一个工件下面的工序有先后顺序,所以有的节点之间会增加蓝色箭头。在同一台机器上加工的工序也必须有先有后,所以也要有箭头, 因此每一对红绿箭头必须去掉其中一个,保留其中一个,这就会对应了四种可能的可行解的图。
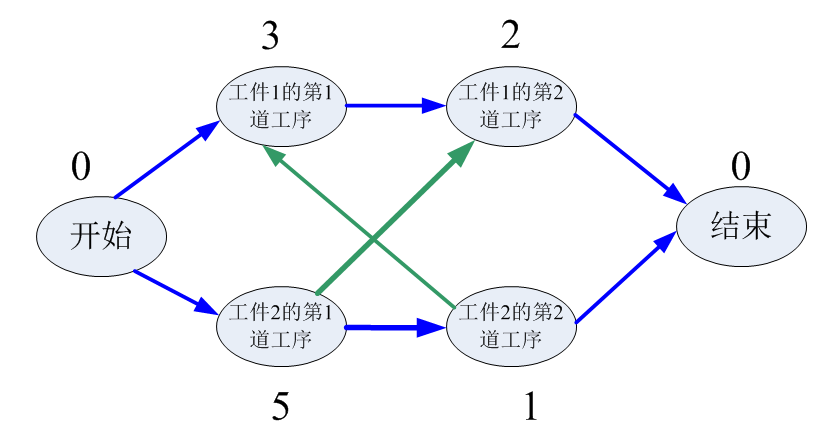
可行解1的图
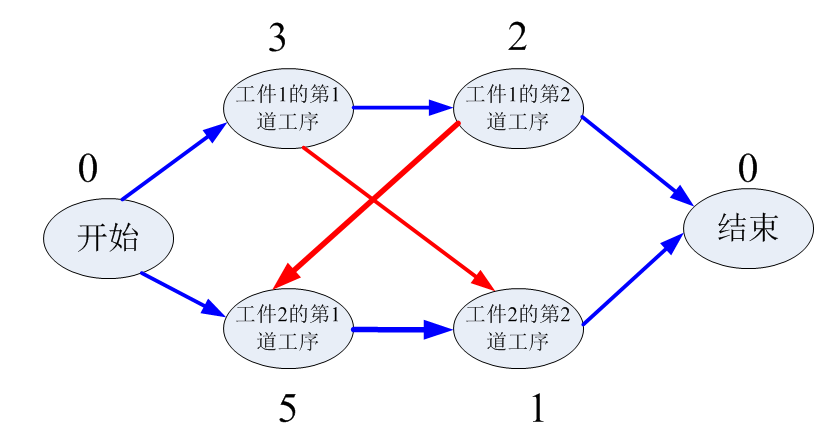
可行解2的图
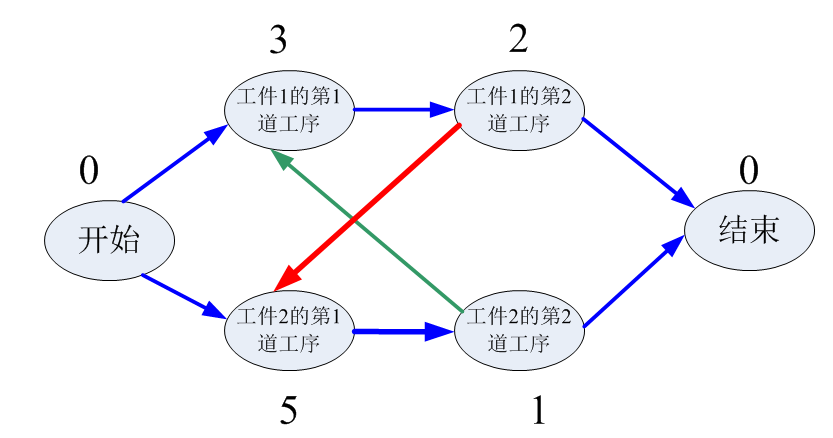
可行解3的图
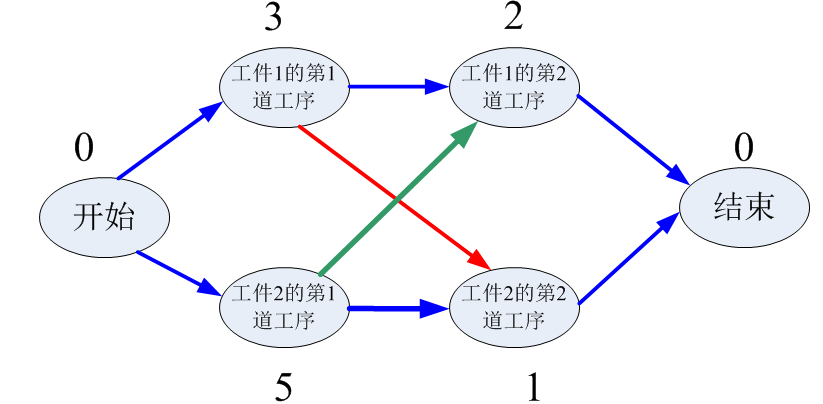
可行解4的图
上面的四种方案都可行,每个可行解都有一个总完成时间,即所有从开始节点到结束节点的路径中权值之和最大的那条路径对应的权值之和。我们的目标是从四个可行的解中找到一个最优解,最优解是总完成时间最短的那个解,例如:可行解1需要11个单位总完成时间,可行解2需要11个单位总完成时间,可行解3需要11个单位总完成时间,可行解4需要7个单位总完成时间。显然,最优解就是可行解4,在可行解4中工件1的工序1的开始时间是0,工件2的工序1的开始时间是0,工件1的工序2的开始时间是5,工件2的工序2的开始时间是5。总完成时间是7。
编码
我们利用工件号的排列来对可行解进行编码,例如:1212这个编码中第一个1代表第1个工件的第1道工序,第二个1代表第1个工件的第2道工序,第1个2代表第2个工件的第1道工序,第2个2代表第2个工件的第2道工序。在这个编码中潜藏着:工件1的第1道工序要在工件2的第2道工序之前,工件2的第1道工序要在工件1的第2道工序之前。这个编码对应的是可行解4。需要说明的是一个可行解的有向无环图可能对应多个编码方式,例如,1212,2121,1221,2112都对应上面的可行解4的有向无环图。
解码
一个最简单的求最优解的思路就是:把所有可能的编码都列出来(即两个1与两个2能组成的所有排列),然后利用已知条件表格把每个编码对应的可行解图都还原出来,利用该可行解图计算出该可行解对应的总完成时间,从所有可行解中找到总完成时间最短的。上文中已经说明了总完成时间就是可行解图之中从开始节点到结束节点间所有路径中权值之和最大的那条路径的权值和。如何在带权无环有向图中找到权值和最大的那条从起点到终点的关键路径(critical path),可以参考简书中的文章:https://www.jianshu.com/p/cef14f70ec92。