Mister B and PR Shifts 思维

题目

Some time ago Mister B detected a strange signal from the space, which he started to study.

After some transformation the signal turned out to be a permutation pp of length nn or its cyclic shift. For the further investigation Mister B need some basis, that's why he decided to choose cyclic shift of this permutation which has the minimum possible deviation.

Let's define the deviation of a permutation pp as .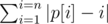

Find a cyclic shift of permutation pp with minimum possible deviation. If there are multiple solutions, print any of them.

Let's denote id kk ( 0<=k<n ) of a cyclic shift of permutation pp as the number of right shifts needed to reach this shift, for example:

• k=0k=0 : shift p_{1},p_{2},... p_{n}p1,p2,... p**n ,
• k=1k=1 : shift p_{n},p_{1},... p_{n-1}p**n,p1,... p**n−1 ,
• ...,
• k=n-1k=n−1 : shift p_{2},p_{3},... p_{n},p_{1}p2,p3,... p**n,p1 .

输入格式

First line contains single integer nn ( 2<=n<=10^{6}2<=n<=106 ) — the length of the permutation.

The second line contains nn space-separated integers p_{1},p_{2},...,p_{n}p1,p2,...,p**n ( 1<=p_{i}<=n1<=p**i<=n ) — the elements of the permutation. It is guaranteed that all elements are distinct.

输出格式

Print two integers: the minimum deviation of cyclic shifts of permutation pp and the id of such shift. If there are multiple solutions, print any of them.

题意翻译

• 定义一个全排列p_ip**i的偏移值为sum_{i=1}^n|p_i-i|∑i=1n∣p**i−i∣
• 给你一个全排列，你可以从后面拿kin[0,n-1]k∈[0,n−1]个数放在前面，使得该全排列的偏移值最小，输出这个偏移值和k，如果有多个k任意输出一个
• nleq 10^6n≤106

输入输出样例

输入 #1复制

3
1 2 3

输出 #1复制

0 0

输入 #2复制

3
2 3 1

输出 #2复制

0 1

输入 #3复制

3
3 2 1

输出 #3复制

2 1

说明/提示

In the first sample test the given permutation pp is the identity permutation, that's why its deviation equals to 00 , the shift id equals to 00 as well.

In the second sample test the deviation of pp equals to 44 , the deviation of the 11 -st cyclic shift (1,2,3)(1,2,3) equals to 00 , the deviation of the 22 -nd cyclic shift (3,1,2)(3,1,2) equals to 44 , the optimal is the 11 -st cyclic shift.

In the third sample test the deviation of pp equals to 44 , the deviation of the 11 -st cyclic shift (1,3,2)(1,3,2) equals to 22 , the deviation of the 22 -nd cyclic shift (2,1,3)(2,1,3) also equals to 22 , so the optimal are both 11 -st and 22 -nd cyclic shifts.

分析

每次右移，(|p[i]-i|)的值要不就加1，要不就减1。

可以通过两个变量l，r来记录每次右移加1的个数和减1的个数

再定义(t[i])表示初始数组中有多少个数在它目标左边的第i个位置

每次l-=t[i-1],r+=t[i-1]

每次右移这个式子的和sum为sum-l+r-1- (n-p[n-i+1])+(p[n-i+1]-1)

/*************************************************************************
	> File Name: k.cpp
	> Author: LiuGeXian
	> Mail: 1019630230@qq.com 
	> Created Time: 2020/5/8 22:35:41
 ************************************************************************/

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 5;
int n, m, p[maxn], l, r, t[maxn];
int sum;
int k;
int main(){
	scanf("%d", &n);
	for (int i = 1; i <= n; i++){
		scanf("%d", &p[i]);
		sum += abs(i - p[i]);
		if (p[i] >= i){
			l++;
			t[p[i]-i]++;
		}
		else r++;
	}
	int ans = sum;
	for (int i = 1; i < n; i++){
		l -= t[i-1];
		r += t[i-1];
		sum = sum - l + r - 1 - (n - p[n-i+1]) + (p[n-i+1] - 1);
		l++;
		r--;
		t[p[n-i+1]+i-1]++;
		if (sum < ans){
			ans = sum;
			k = i;
		}
	}
	cout << ans << ' ' << k;
	return 0;
}