数据结构与算法-散列

散列的引入

考虑下面的问题

给出N个正整数，再给出M个正整数，其中N，M<=10⁵，问M中的每个数是否在N中出现过？

最直观的解法：首先需要把N个数据存储起来，然后遍历M个数据，拿到每个M后，再遍历N，判断是否存在一个数与当前待判断数相等，时间复杂度为O(NM)。

有一种空间换时间的解法：有一个大小为10⁵的数组，数组中存储bool变量。读取N的时候，以N中的数作为数组下标，把数组下标对应位置的bool变量设置为true。再遍历M，把M中的数作为数组下标直接随机访问，如果为true，代表出现过。时间复杂度O(N+M)。

c实现

#include <stdio.h>

bool hashtable[100000] = {false};

void hashSearch(){
    int n = 0, m = 0;
    int tmp = 0;
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; ++i) {
        scanf("%d", &tmp);
        hashtable[tmp] = true;
    }
    for (int i = 0; i < m; ++i) {
        scanf("%d", &tmp);
        if (hashtable[tmp]) {
            printf("%d,YES
", tmp);
        } else {
            printf("%d,NO
", tmp);
        }
    }
}

int main() {
    hashSearch();
    return 0;
}

---

散列的定义

上面的做法，通过把输入的数字作为数组下标来对数字的某些性质进行统计，后续再查询时，也是通过数组的随机访问直接定位，查找效率很高。

但是现实中，首先数字可能很大，或者输入的是字符串，不能直接作为数组下标了，如何处理？

散列 关注的就是这个转换的过程，进一步说，散列使元素通过一个函数转换为整数，并使得该整数尽可能唯一的代表这个元素。

散列函数

如果待散列的元素为整数，有以下常见的散列函数：

• 直接定址法：采用 元素本身 （上面例题中的做法）或者元素的线性函数来定址，适合表元素数量较小的情况。
• 数字分析法：分析待散列元素数字，通过抽取部分分布均匀的数字来作为散列地址，适合元素本身位数较大，并且数字分布有规律的情况。（比如手机号，身份证号等等）
• 平方取中法：数字平方后，取中间的N位，适合 位数不大，不知道数据分布的情况
• 叠加求和法：把一个多位数字按照位数 切割 分成多个数字，这些数字求和，取模。适合位数较大，不知道数据分布的情况
• 除留余数法：取模得到散列地址，需要注意，除数尽量选择 小于等于表长的 素数。

如果带散列的元素为字符串，介绍一个散列函数，进制hash法：

假设字符中只包含A到Z这26个大写字母，A到Z可以视为0到25，那么这个字符串可以看作是一个26进制的数，将26进制转换为10进制，就得到了一个整数。

从N进制转换为十进制的算法这里就不再细说，假设读者已经有了这个基础。

上面的字符串hash，可以转换为下面的C实现代码：

void hashFunc(char str[]) {
    int id = 0;
    for (int i = 0; i < strlen(str); ++i) {
        id = id * 26 + (str[i] - 'A');
    }
    printf("%s", id);
}

重点解释一下下面这行

 id = id * 26 + (str[i] - 'A');

以一个字符串“ZZZ”为例，计算过程如下:

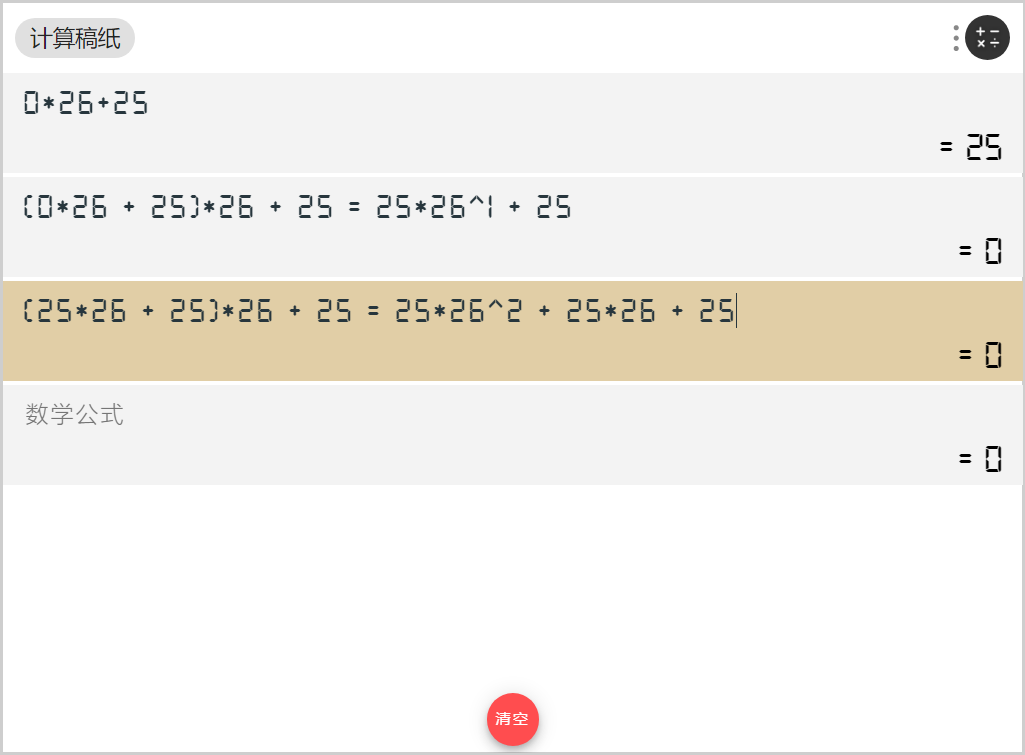
可以看到，这个公式最终可以转换为N进制转换为10进制的公式。