题目:https://www.luogu.org/problemnew/show/3958
题目描述
现有一块大奶酪,它的高度为 hh,它的长度和宽度我们可以认为是无限大的,奶酪 中间有许多 半径相同 的球形空洞。我们可以在这块奶酪中建立空间坐标系,在坐标系中, 奶酪的下表面为z=0,奶酪的上表面为z=h。
现在,奶酪的下表面有一只小老鼠 Jerry,它知道奶酪中所有空洞的球心所在的坐 标。如果两个空洞相切或是相交,则 Jerry 可以从其中一个空洞跑到另一个空洞,特别 地,如果一个空洞与下表面相切或是相交,Jerry 则可以从奶酪下表面跑进空洞;如果 一个空洞与上表面相切或是相交,Jerry 则可以从空洞跑到奶酪上表面。
位于奶酪下表面的 Jerry 想知道,在 不破坏奶酪 的情况下,能否利用已有的空洞跑 到奶酪的上表面去?
空间内两点P1(x1,y1,z1)、P2(x2,y2,z2)的距离公式如下:
dist(P1,P2)=sqrt((x1−x2)^2+(y1−y2)^2+(z1−z2)^2)
输入输出格式
输入格式:
每个输入文件包含多组数据。
输入文件的第一行,包含一个正整数 T,代表该输入文件中所含的数据组数。
接下来是 T 组数据,每组数据的格式如下: 第一行包含三个正整数n,h 和 r,两个数之间以一个空格分开,分别代表奶酪中空 洞的数量,奶酪的高度和空洞的半径。
接下来的 n 行,每行包含三个整数x,y,z,两个数之间以一个空格分开,表示空 洞球心坐标为(x,y,z)。
输出格式:
输出文件包含 T 行,分别对应 T 组数据的答案,如果在第 i 组数据中,Jerry 能从下 表面跑到上表面,则输出Yes,如果不能,则输出No (均不包含引号)。
输入输出样例
说明
【输入输出样例 1 说明】
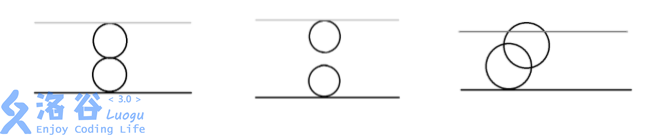
第一组数据,由奶酪的剖面图可见:
第一个空洞在(0,0,0)与下表面相切
第二个空洞在(0,0,4)与上表面相切 两个空洞在(0,0,2)相切
输出 Yes
第二组数据,由奶酪的剖面图可见:
两个空洞既不相交也不相切
输出 No
第三组数据,由奶酪的剖面图可见:
两个空洞相交 且与上下表面相切或相交
输出 Yes
【数据规模与约定】
对于 20%的数据,n=1,1≤h,r≤10,000,坐标的绝对值不超过 10,000。
对于 40%的数据,1≤n≤8, 1≤h,r≤10,000,坐标的绝对值不超过 10,000。
对于80%的数据,1≤n≤1,000,1≤h,r≤10,000,坐标的绝对值不超过10,000。
对于 100%的数据,1≤n≤1,000,1≤h,r≤1,000,000,000,T≤20,坐标的 绝对值不超过 1,000,000,000。
解析
直接一波大爆搜走起啊。。。。。。
D2T1送分来啦。

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cmath> 6 #include<vector> 7 using namespace std; 8 #define ll long long 9 #define maxn 1010 10 int t; 11 int n; 12 double h,r; 13 double x[maxn],y[maxn],z[maxn]; 14 bool vis[maxn],ok; 15 vector<int> s; 16 bool check(int a,int b){ 17 if ((x[a]-x[b])*(x[a]-x[b])+(y[a]-y[b])*(y[a]-y[b])+(z[a]-z[b])*(z[a]-z[b])<=4*r*r){ 18 return true; 19 }else{ 20 return false; 21 } 22 } 23 bool dfs(int x){ 24 if (abs(h-z[x])<=r){ 25 return true; 26 } 27 bool ans=false; 28 for (int i=1;i<=n;++i){ 29 if (vis[i]) continue; 30 if (check(x,i)){ 31 vis[i]=true; 32 if (dfs(i)){ 33 ans=true; 34 break; 35 } 36 } 37 } 38 return ans; 39 } 40 int main(){ 41 //freopen("cheese.in","r",stdin); 42 //freopen("cheese.out","w",stdout); 43 scanf("%d",&t); 44 while (t--){ 45 s.clear(); 46 ok=false; 47 memset(vis,false,sizeof(vis)); 48 scanf("%d%lf%lf",&n,&h,&r); 49 for (int i=1;i<=n;++i){ 50 scanf("%lf%lf%lf",&x[i],&y[i],&z[i]); 51 if (z[i]<=r) s.push_back(i); 52 } 53 for (int i=0;i<s.size();++i){ 54 int ss=s[i]; 55 if (vis[ss]) continue; 56 if (dfs(ss)){ 57 ok=true; 58 break; 59 } 60 } 61 if (ok) printf("Yes "); 62 else printf("No "); 63 } 64 //fclose(stdin); 65 //fclose(stdout); 66 return 0; 67 }
