1、介绍
在前一篇博客中我们学习了广度优先搜索算法,它解决的是段数最少的路径,如果你要找到最快的路径,该怎么办呢?为此,可以使用本篇博客所讲述的算法——狄克斯特拉算法
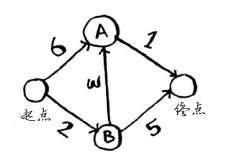
如果你使用广度优先搜索,将得到下面这条段数最少的路径。
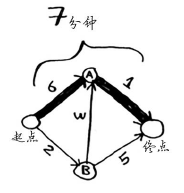
这条路径耗时7分钟。下面来看看能否找到耗时更短的路径!狄克斯特拉算法包含4个步骤。
(1) 找出“最便宜”的节点,即可在最短时间内到达的节点。
(2) 更新该节点的邻居的开销,其含义将稍后介绍。
(3) 重复这个过程,直到对图中的每个节点都这样做了。
(4) 计算最终路径。
第一步:找出最便宜的节点。你站在起点,不知道该前往节点A还是前往节点B。前往这两个节点都要多长时间呢?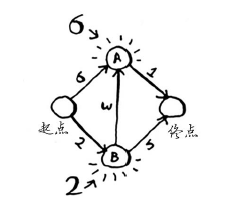
前往节点A需要6分钟,而前往节点B需要2分钟。至于前往其他节点,你还不知道需要多长时间。
由于你还不知道前往终点需要多长时间,因此你假设为无穷大(这样做的原因你马上就会明白)。节点B是最近的——2分钟就能达到。
第二步:计算经节点B前往其各个邻居所需的时间。
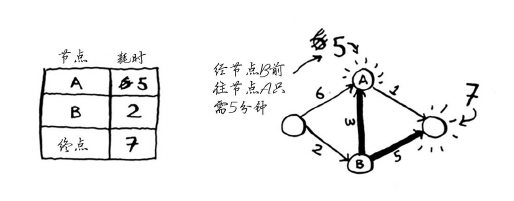
你刚找到了一条前往节点A的更短路径!直接前往节点A需要6分钟。
对于节点B的邻居,如果找到前往它的更短路径,就更新其开销。在这里,你找到了:
- 前往节点A的更短路径(时间从6分钟缩短到5分钟);
- 前往终点的更短路径(时间从无穷大缩短到7分钟)。
第三步:重复!
重复第一步:找出可在最短时间内前往的节点。你对节点B执行了第二步,除节点B外,可在最短时间内前往的节点是节点A。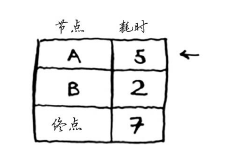
重复第二步:更新节点A的所有邻居的开销。
你发现前往终点的时间为6分钟!
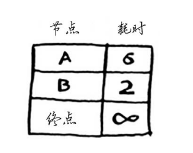
你对每个节点都运行了狄克斯特拉算法(无需对终点这样做)。现在,你知道:
- 前往节点B需要2分钟;
- 前往节点A需要5分钟;
- 前往终点需要6分钟。
狄克斯特拉算法包含4个步骤。
(1) 找出最便宜的节点,即可在最短时间内前往的节点。
(2) 对于该节点的邻居,检查是否有前往它们的更短路径,如果有,就更新其开销。
(3) 重复这个过程,直到对图中的每个节点都这样做了。
(4) 计算最终路径。
二、换钢琴
Rama想拿一本乐谱换架钢琴。
Alex说:“这是我最喜欢的乐队Destroyer的海报,我愿意拿它换你的乐谱。如果你再加5美元,还可拿乐谱换我这张稀有的Rick Astley黑胶唱片。”Amy说:“哇,我听说这张黑胶唱片里有首非常好听的歌曲,我愿意拿我的吉他或架子鼓换这张海报或黑胶唱片。”
Beethoven惊呼:“我一直想要吉他,我愿意拿我的钢琴换Amy的吉他或架子鼓。”
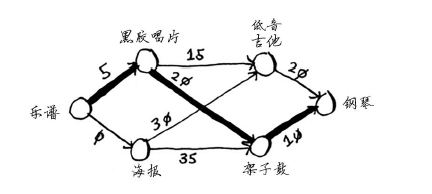
太好了!只要再花一点点钱,Rama就能拿乐谱换架钢琴。现在他需要确定的是,如何花最少的钱实现这个目标。我们来绘制一个图,列出大家的交换意愿。
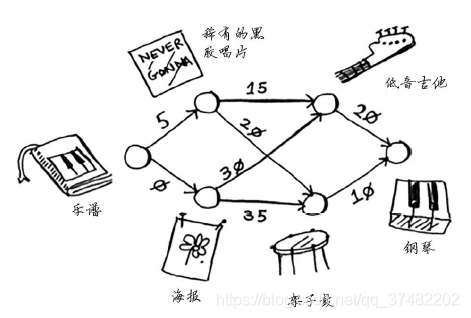
这个图中的节点是大家愿意拿出来交换的东西,边的权重是交换时需要额外加多少钱。拿海报换吉他需要额外加30美元,拿黑胶唱片换吉他需要额外加15美元。Rama需要确定采用哪种路径将乐谱换成钢琴时需要支付的额外费用最少。为此,可以使用狄克斯特拉算法!别忘了,狄克斯特拉算法包含四个步骤。在这个示例中,你将完成所有这些步骤,因此你也将计算最终路径。动手之前,你需要做些准备工作:创建一个表格,在其中列出每个节点的开销。这里的开销指的是达到节点需要额外支付多少钱。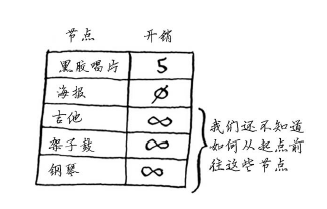
在执行狄克斯特拉算法的过程中,你将不断更新这个表。为计算最终路径,还需在这个表中添加表示父节点的列。

第一步:找出最便宜的节点。在这里,换海报最便宜,不需要支付额外的费用。还有更便宜的换海报的途径吗?这一点非常重要,你一定要想一想。Rama能够通过一系列交换得到海报,还能额外得到钱吗?答案是不能,因为海报是Rama能够到达的最便宜的节点,没法再便宜了。
第二步:计算前往该节点的各个邻居的开销。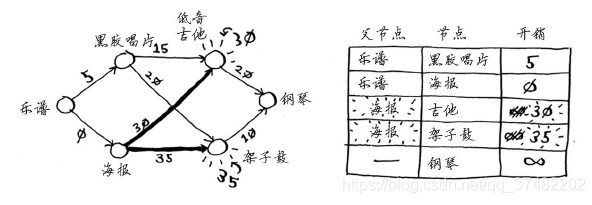
现在的表中包含低音吉他和架子鼓的开销。这些开销是用海报交换它们时需要支付的额外费用,因此父节点为海报。这意味着,要到达低音吉他,需要沿从海报出发的边前行,对架子鼓来说亦如此。

再次执行第一步:下一个最便宜的节点是黑胶唱片——需要额外支付5美元。
再次执行第二步:更新黑胶唱片的各个邻居的开销。

你更新了架子鼓和吉他的开销!这意味着经“黑胶唱片”前往“架子鼓”和“吉他”的开销更低,因此你将这些乐器的父节点改为黑胶唱片。下一个最便宜的是吉他,因此更新其邻居的开销。
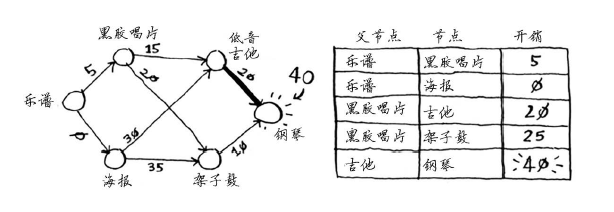
你终于计算出了用吉他换钢琴的开销,于是你将其父节点设置为吉他。最后,对最后一个节点——架子鼓,做同样的处理。
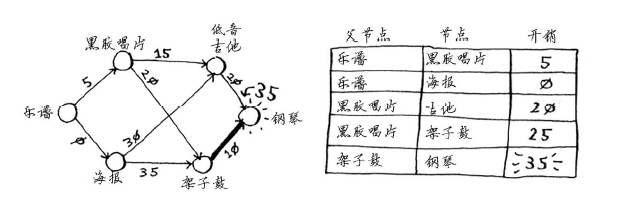
如果用架子鼓换钢琴,Rama需要额外支付的费用更少。因此,采用最便宜的交换路径时,Rama需要额外支付35美元。
现在来兑现前面的承诺,确定最终的路径。当前,我们知道最短路径的开销为35美元,但如何确定这条路径呢?为此,先找出钢琴的父节点。
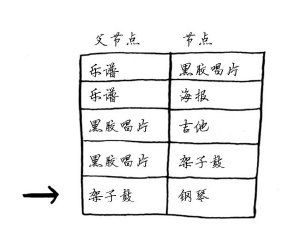
钢琴的父节点为架子鼓,这意味着Rama需要用架子鼓来换钢琴。因此你就沿着这一边。
我们来看看需要沿哪些边前行。钢琴的父节点为架子鼓。

架子鼓的父节点为黑胶唱片。
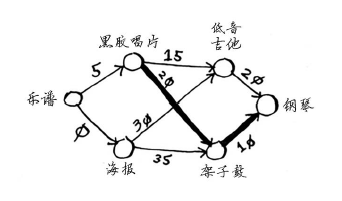
因此Rama需要用黑胶唱片了换架子鼓。显然,他需要用乐谱来换黑胶唱片。通过沿父节点回溯,便得到了完整的交换路径。
三、注意
有向无环图
图还可能有环,这意味着你可从一个节点出发,走一圈后又回到这个节点。假设在下面这个带环的图中,你要找出从起点到终点的最短路径。
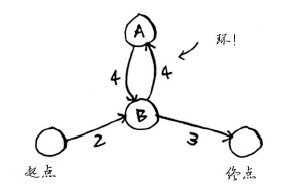
绕环前行是否合理呢?你可以选择避开环的路径。

也可选择包含环的路径:
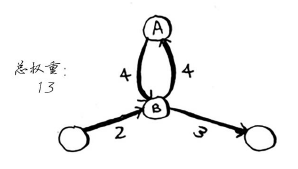
这两条路径都可到达终点,但环增加了权重。如果你愿意,甚至可绕环两次。
但每绕环一次,总权重都增加8。因此,绕环的路径不可能是最短的路径。
无向图意味着两个节点彼此指向对方,其实就是环!
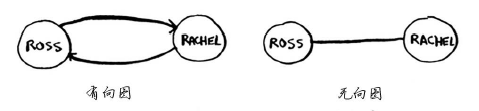
在无向图中,每条边都是一个环。狄克斯特拉算法只适用于有向无环图。
负权边
回到上面换钢琴的例子,假设黑胶唱片不是Alex的,而是Sarah的,且Sarah愿意用黑胶唱片和7美元换海报。换句话说,换得Alex的海报后,Rama用它来换Sarah的黑胶唱片时,不但不用支付额外的费用,还可得7美元。对于这种情况,如何在图中表示出来呢?
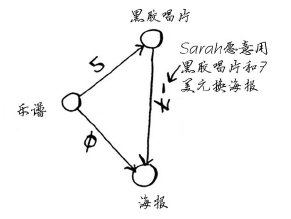
从黑胶唱片到海报的边的权重为负!即这种交换让Rama能够得到7美元。现在,Rama有两种获得海报的方式。
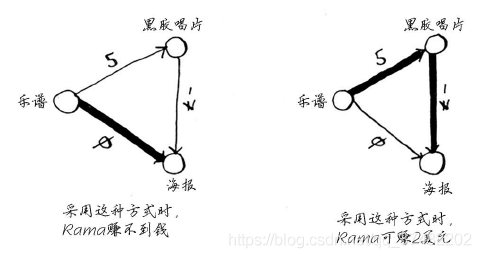
第二种方式更划算——Rama可赚2美元!你可能还记得,Rama可以用海报换架子鼓,但现在有两种换得架子鼓的方式。
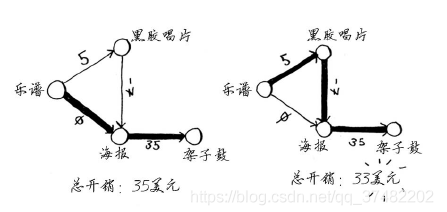
第二种方式的开销少2美元,他应采取这种方式。然而,如果你对这个图运行狄克斯特拉算法,Rama将选择错误的路径——更长的那条路径。如果有负权边,就不能使用狄克斯特拉算法。因为负权边会导致这种算法不管用。下面来看看对这个图执行狄克斯特拉算法的情况。首先,创建开销表。
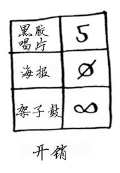
接下来,找出开销最低的节点,并更新其邻居的开销。在这里,开销最低的节点是海报。根据狄克斯特拉算法,没有比不支付任何费用获得海报更便宜的方式。(你知道这并不对!)无论如何,我们来更新其邻居的开销。
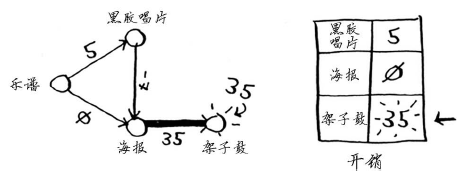
现在,架子鼓的开销变成了35美元。
我们来找出最便宜的未处理节点。

更新其邻居的开销。
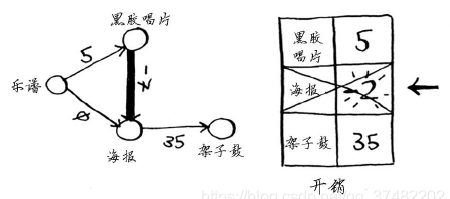
海报节点已处理过,这里却更新了它的开销。这是一个危险信号。节点一旦被处理,就意味着没有前往该节点的更便宜途径,但你刚才却找到了前往海报节点的更便宜途径!架子鼓没有任何邻居,因此算法到此结束,最终开销如下。
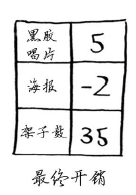
换得架子鼓的开销为35美元。你知道有一种交换方式只需33美元,但狄克斯特拉算法没有找到。这是因为狄克斯特拉算法这样假设:对于处理过的海报节点,没有前往该节点的更短路径。这种假设仅在没有负权边时才成立。因此,不能将狄克斯特拉算法用于包含负权边的图。在包含负权边的图中,要找出最短路径,可使用另一种算法——贝尔曼-福德算法,你可以在网上找到其详尽的说明。
四、实现
有这样的一条道路,你现在在A点,想要前往H点,请找出最短路径:
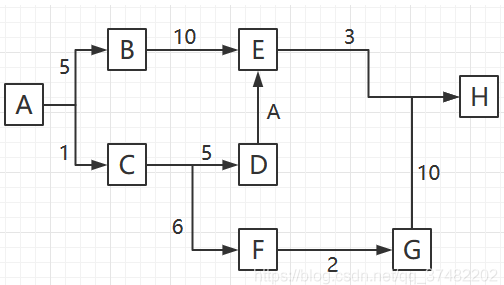
想要使用JAVA构造有向图的数据结构,你可以使用HashMap嵌套,
HashMap<String, HashMap<String, Integer>>
外层String代表节点名称,内层hashmap代表改节点可前往的点,内部hashmap的String代表外层点可到达的点的名称,Integer代表路程
按照上述步骤书写代码,如下:
1 import java.util.ArrayList; 2 import java.util.HashMap; 3 import java.util.List; 4 5 public class Dijkstra { 6 public static void main(String[] args) { 7 HashMap<String, Integer> A = new HashMap<String, Integer>() { 8 { 9 put("B", 5); 10 put("C", 1); 11 } 12 }; 13 14 HashMap<String, Integer> B = new HashMap<String, Integer>() { 15 { 16 put("E", 10); 17 } 18 }; 19 HashMap<String, Integer> C = new HashMap<String, Integer>() { 20 { 21 put("D", 5); 22 put("F", 6); 23 } 24 }; 25 HashMap<String, Integer> D = new HashMap<String, Integer>() { 26 { 27 put("E", 3); 28 } 29 }; 30 HashMap<String, Integer> E = new HashMap<String, Integer>() { 31 { 32 put("H", 3); 33 } 34 }; 35 HashMap<String, Integer> F = new HashMap<String, Integer>() { 36 { 37 put("G", 2); 38 } 39 }; 40 HashMap<String, Integer> G = new HashMap<String, Integer>() { 41 { 42 put("H", 10); 43 } 44 }; 45 HashMap<String, HashMap<String, Integer>> allMap = new HashMap<String, HashMap<String, Integer>>() { 46 { 47 put("A", A); 48 put("B", B); 49 put("C", C); 50 put("D", D); 51 put("E", E); 52 put("F", F); 53 put("G", G); 54 } 55 }; 56 57 58 Dijkstra dijkstra = new Dijkstra(); 59 dijkstra.handle("A", "H", allMap); 60 } 61 62 private String getMiniCostKey(HashMap<String, Integer> costs, List<String> hasHandleList) { 63 int mini = Integer.MAX_VALUE; 64 String miniKey = null; 65 for (String key : costs.keySet()) { 66 if (!hasHandleList.contains(key)) { 67 int cost = costs.get(key); 68 if (mini > cost) { 69 mini = cost; 70 miniKey = key; 71 } 72 } 73 } 74 return miniKey; 75 } 76 77 private void handle(String startKey, String target, HashMap<String, HashMap<String, Integer>> all) { 78 //存放到各个节点所需要消耗的时间 79 HashMap<String, Integer> costMap = new HashMap<String, Integer>(); 80 //到各个节点对应的父节点 81 HashMap<String, String> parentMap = new HashMap<String, String>(); 82 //存放已处理过的节点key,已处理过的不重复处理 83 List<String> hasHandleList = new ArrayList<String>(); 84 85 //首先获取开始节点相邻节点信息 86 HashMap<String, Integer> start = all.get(startKey); 87 88 //添加起点到各个相邻节点所需耗费的时间等信息 89 for (String key : start.keySet()) { 90 int cost = start.get(key); 91 costMap.put(key, cost); 92 parentMap.put(key, startKey); 93 } 94 95 96 //选择最"便宜"的节点,这边即耗费时间最低的 97 String minCostKey = getMiniCostKey(costMap, hasHandleList); 98 while (minCostKey != null) { 99 System.out.print("处理节点:" + minCostKey); 100 HashMap<String, Integer> nodeMap = all.get(minCostKey); 101 if (nodeMap != null) { 102 //该节点没有子节点可以处理了,末端节点 103 handleNode(minCostKey, nodeMap, costMap, parentMap); 104 } 105 //添加该节点到已处理结束的列表中 106 hasHandleList.add(minCostKey); 107 //再次获取下一个最便宜的节点 108 minCostKey = getMiniCostKey(costMap, hasHandleList); 109 } 110 if (parentMap.containsKey(target)) { 111 System.out.print("到目标节点" + target + "最低耗费:" + costMap.get(target)); 112 List<String> pathList = new ArrayList<String>(); 113 String parentKey = parentMap.get(target); 114 while (parentKey != null) { 115 pathList.add(0, parentKey); 116 parentKey = parentMap.get(parentKey); 117 } 118 pathList.add(target); 119 String path = ""; 120 for (String key : pathList) { 121 path = path + key + " --> "; 122 } 123 System.out.print("路线为" + path); 124 } else { 125 System.out.print("不存在到达" + target + "的路径"); 126 } 127 } 128 129 private void handleNode(String startKey, HashMap<String, Integer> nodeMap, HashMap<String, Integer> costMap, HashMap<String, String> parentMap) { 130 131 for (String key : nodeMap.keySet()) { 132 //获取原本到父节点所需要花费的时间 133 int hasCost = costMap.get(startKey); 134 //获取父节点到子节点所需要花费的时间 135 int cost = nodeMap.get(key); 136 //计算从最初的起点到该节点所需花费的总时间 137 cost = hasCost + cost; 138 139 if (!costMap.containsKey(key)) { 140 //如果原本并没有计算过其它节点到该节点的花费 141 costMap.put(key, cost); 142 parentMap.put(key, startKey); 143 } else { 144 //获取原本耗费的时间 145 int oldCost = costMap.get(key); 146 if (cost < oldCost) { 147 //新方案到该节点耗费的时间更少 148 //更新到达该节点的父节点和消费时间对应的散列表 149 costMap.put(key, cost); 150 parentMap.put(key, startKey); 151 System.out.print("更新节点:" + key + ",cost:" + oldCost + " --> " + cost); 152 } 153 } 154 } 155 } 156 } 157
六:参考致谢
部分图片和内容摘自如下博客,主要内容来自《图解算法》。
1. https://blog.csdn.net/qq_37482202/article/details/89546951
Over......