无符号数和有符号数

1.      补码

在计算机中无符号数用原码表示，有符号数用补码表示。w位补码表示的值为:

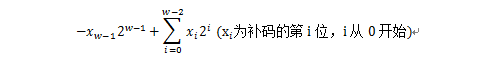
最高位 也称符号位，1表示负数，0表示正数，符号位为0时，和无符号数的表示是相同的，以下是4位补码的示例：

0101 = -0*2³ + 1*2² + 0*2¹ + 1*2⁰ = 5

1101 = -1*2³ + 1*2² + 0*2¹ + 1*2⁰ = -3

w位的补码表示的数值范围是[-2^w-1, 2^w-1-1]，如4位的补码表示的最小值是-8（1000），最大值是7（0111）。

只有理解了有符号数的补码表示，才能真正理解无符号数和有符号数的转换、有符号数的截断和溢出等问题。

2.      无符号数和有符号数的转换

C语言中的强制类型转换保持二进制位值不变，只是改变解释位的方式。看以下代码：

short int v = -12345;

unsigned short uv = (unsigned short)v;

printf(“v = %d, uv = %u ”, u, uv);

输出如下：

v = -12345, uv = 53191

由于-12345的16位补码表示与53191的16位无符号表示是完全一样的，所以会得到以上输出。

无符号数和有符号数之间的转换是一一对应的关系，w位的有符号数s转换无符号数u的对应关系为：

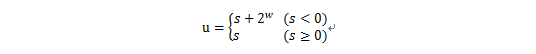
如4位有符号数7（0111）转换为无符号数也是7，而4位有符号数-1（1111）转换为无符号数是15。

类似地，w位的无符号数u转换为有符号数s的对应关系为：

如4位无符号数5（0101）转换为无符号数也是5，而4位无符号数13（1101）转换为无符号数为-3。

其实只要知道无符号数和有符号数对二进制位的解释方式，无需记住上述的对应关系，也能算出转换后的值。

3.      陷阱

在C语言中，如果一个运算包含一个有符号数和一个无符号数，那么C语言会隐式地将有符号数转换为无符号数，这对于标准的算术运算没什么问题，但是对于 < 和 > 这样的关系运算符来说，它会出现非直观的结果，这种非直观的特性经常会导致程序中难以察觉的错误。看下面的例子：

int strlonger(char *s, char *t)

{

    return strlen(s) - strlen(t) > 0;

}

上面的函数看起来似乎没什么问题，实际上当s比t短时，函数的返回值也是1，为什么会出现这种情况呢？原来strlen的返回值类型为size_t，C语言中将size_t定义为unsigned int，当s比t短时,strlen(s) - strlen(t)为负数，但无符号数的运算结果隐式转换为无符号数就变成了很大的无符号数。为了让函数正确工作，代码应该修改如下：

return strlen(s) > strlen(t);

2002年，从事FreeBSD开源操作系统项目的程序员意识到，他们对getpeername函数的实现存在安全漏洞。代码的简化版本如下：

void *memcpy(void *dest, void *src,  size_t n);

#define KSIZE 1024

char kbuf[KSIZE];

int copy_from_kernel(void *user_dest, int maxlen)

{

    int len = KSIZE < maxlen ? KSIZE : maxlen;

    memcpy(user_dest, kbuf, len);

    retn len;

}

你看出了问题所在吗？

4.      扩展、截断和溢出

将无符号数转换为更大的数据类型时，只需简单地在开头添加0，这种运算称为0扩展。将有符号数转换为更大的数据类型需要执行符号扩展，规则是将符号位扩展至所需要的位数。如将4位的二进制数1001（-7）扩展为8位的结果为11111001（-7）。

将一个大的数据类型转换为小的数据类型时，不管是无符号数还是有符号数都是简单地进行位截断。无符号数的数值大小可能因截断而变化，而有符号数不仅数值大小可能变化，符号位也可能发生改变，如8位二进制数00011001（25）转换为4位数截断的结果是1001（-7）。

在进行整数的算术运算时，当结果变量的位数不足以存放实际实际结果的位数时，运算的结果就会因截断而产生溢出，如果4位二进制数运算1011(-5) + 1011(-5) = 10110(-10)，但如果结果也采用4位二进制存放就会截断为0110（6），产生溢出。

当数据类型转换时，同时需要在不同数据大小，以及无符号和有符号之间转换时，C语言标准要求先进行数据大小的转换，之后再进行无符号和有符号之间的转换。