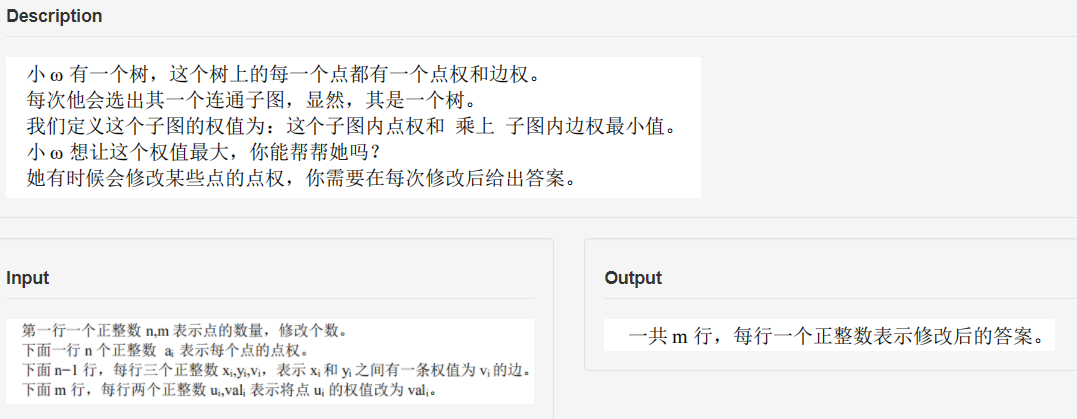
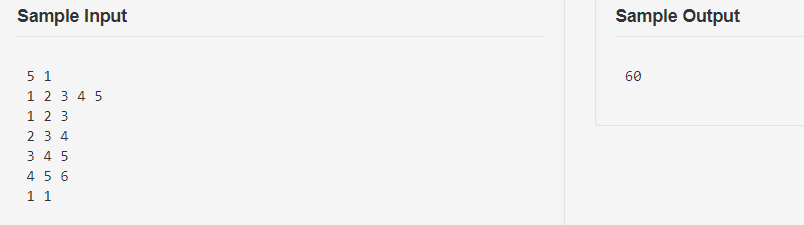
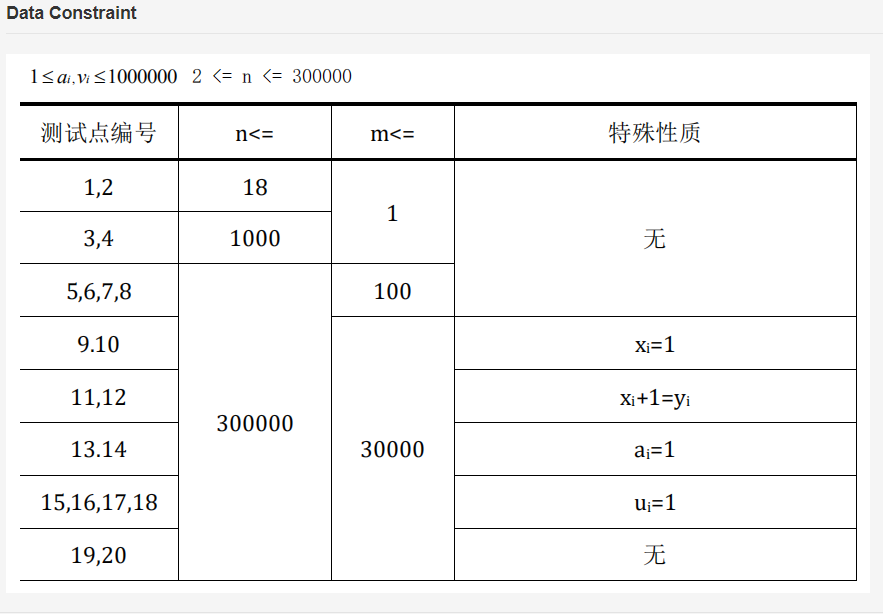
题目描述
题解
qy的毒瘤题
CSP搞这种码农题当场手撕出题人
先按照边权从大到小建重构树,然后40%暴力修改+查找即可
100%可以定期重构+平衡规划,每次把B个询问拉出来建虚树,在虚树上暴力维护每一段的凸壳,在凸壳上二分
虚树建法:
按照dfs序排序,每次用栈维护从根到当前点的栈
每次把当前点和栈顶做lca,若lca=栈顶就直接加,否则一直弹到栈顶是lca的祖先,顺便记录下每个点在虚树上的父亲
如果栈顶=之前的lca就不用管,否则加上lca,修改最后弹出的点的父亲
(注意要把根加进去)
设每次搞B个询问,那么时间为(O(QBlog n+frac{Qn}{B})),极限数据下函数长这样:
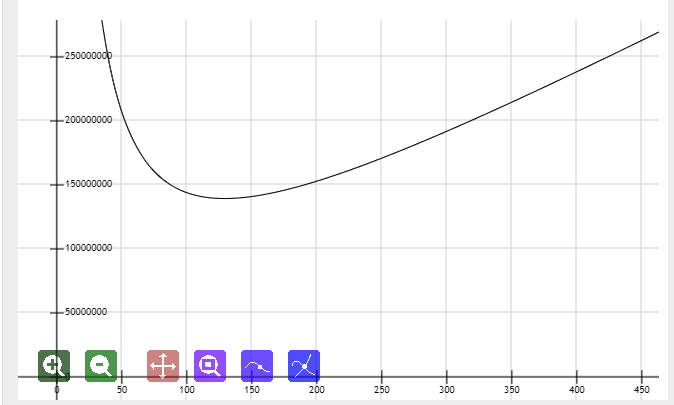
可以看出,实际最优的B为(sqrt{frac{n}{log n}}),但由于常数等原因这样取会被卡成SB
所以B取(sqrt{n})就可以过了(
code
#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define inc(x,y) (bg[x]<=bg[y] && ed[y]<=ed[x])
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
using namespace std;
struct type{
int x,y,s;
} b[300001];
struct Type{
int x,s,id;
} A[30001];
int c[600001];
int C[2001];
long long d[600001][2];
double dx[600001];
int l2[600001];
int r2[600001];
int w[600001];
int v[600001]; //bian
long long sum[600001];
int fa[600001][20];
int fa2[600001];
int son[600001][2];
int bg[600001];
int ed[600001];
int D[600001];
int Fa[600001];
long long ans[30001];
bool bz[600001];
int p[2001];
long long X[600001];
long long ANS[600001];
int d2[600001][2];
bool Bz[600001];
int n,Q,B,i,j,k,l,N,L,R,T,I,tot;
long long Ans,S;
bool cmp(type a,type b)
{
return a.s>b.s;
}
bool Cmp(Type a,Type b)
{
return bg[a.x]<bg[b.x];
}
bool Cmp2(Type a,Type b)
{
return a.id<b.id;
}
int gf(int t)
{
int i,t2;
t2=0;
while (Fa[t]!=t)
{
d2[++t2][0]=t;
t=Fa[t];
}
fo(i,1,t2)
Fa[d2[i][0]]=t;
return t;
}
void dfs()
{
int i,j,k,l,T,t2;
t2=1;
d2[1][0]=N;
d2[1][1]=0;
while (t2)
{
T=t2;
if (!d2[t2][1])
{
D[d2[t2][0]]=D[fa[d2[t2][0]][0]]+1;
bg[d2[t2][0]]=++j;
fo(i,1,19)
fa[d2[t2][0]][i]=fa[fa[d2[t2][0]][i-1]][i-1];
}
if (d2[t2][1]<=1)
{
if (son[d2[t2][0]][d2[t2][1]])
{
++t2;
d2[t2][0]=son[d2[T][0]][d2[T][1]];
d2[t2][1]=0;
}
++d2[T][1];
}
else
{
ed[d2[t2][0]]=j;
--t2;
}
}
}
void swap(int &x,int &y)
{
int z=x;
x=y;
y=z;
}
int lca(int x,int y)
{
int i;
if (D[x]<D[y]) swap(x,y);
fd(i,19,0)
if (D[fa[x][i]]>=D[y])
x=fa[x][i];
fd(i,19,0)
if (fa[x][i]!=fa[y][i])
{
x=fa[x][i];
y=fa[y][i];
}
if (x!=y) x=fa[x][0];
return x;
}
void init()
{
int i,j,k,l;
scanf("%d%d",&n,&Q);//B=floor(sqrt((n+n)/(log(n)/log(2)+1)));
B=floor(sqrt(n));
fo(i,1,n)
scanf("%d",&w[i]);
fo(i,1,n-1)
scanf("%d%d%d",&b[i].x,&b[i].y,&b[i].s);
sort(b+1,b+(n-1)+1,cmp);
fo(i,1,n+n-1)
Fa[i]=i;
fo(i,1,n)
sum[i]=w[i];
fo(i,1,n-1)
{
sum[n+i]=sum[gf(b[i].x)]+sum[gf(b[i].y)];
fa[Fa[b[i].x]][0]=n+i;
fa[Fa[b[i].y]][0]=n+i;
son[n+i][0]=Fa[b[i].x];
son[n+i][1]=Fa[b[i].y];
Fa[Fa[b[i].x]]=n+i;
Fa[Fa[b[i].y]]=n+i;
v[n+i]=b[i].s;
}
}
void build() //xushu
{
int i,j,k,l;
sort(A+L,A+R+1,Cmp);
l=1;
p[1]=N,bz[N]=1;
fo(i,L,R)
if (!l || p[l]!=A[i].x)
{
if (!l)
p[++l]=A[i].x;
else
{
k=lca(p[l],A[i].x);
if (k==p[l])
p[++l]=A[i].x,bz[p[l]]=1;
else
{
while (l && !inc(p[l],k))
{
fa2[p[l]]=p[l-1];
--l;
}
if (p[l]!=k)
{
fa2[p[l+1]]=k;
p[++l]=k,bz[k]=1;
}
}
p[++l]=A[i].x,bz[A[i].x]=1;
}
}
fd(i,l,1)
fa2[p[i]]=p[i-1];
sort(A+L,A+R+1,Cmp2);
tot=0;
fo(i,1,N)
if (bz[i])
C[++tot]=i;
}
void dfs2() //others
{
int i,T,t2;
t2=1;
d2[1][0]=N;
d2[1][1]=0;
while (t2)
{
T=t2;
if (!d2[t2][1])
Bz[d2[t2][0]]=bz[d2[t2][0]];
if (d2[t2][1]<=1)
{
if (son[d2[t2][0]][d2[t2][1]])
{
++t2;
d2[t2][0]=son[d2[T][0]][d2[T][1]];
d2[t2][1]=0;
}
++d2[T][1];
}
else
{
if (!Bz[d2[t2][0]])
Ans=max(Ans,sum[d2[t2][0]]*v[d2[t2][0]]);
if (t2>1)
Bz[d2[t2-1][0]]|=Bz[d2[t2][0]];
--t2;
}
}
}
long long find(int t,int x)
{
int i;
long long ans=0;
fo(i,l2[t],r2[t])
ans=max(ans,d[i][0]*x+d[i][1]);
if (l2[t]>r2[t]) return 0;
if (l2[t]==r2[t]) return d[l2[t]][0]*x+d[l2[t]][1];
int l=l2[t],r=r2[t]-1,mid;
while (l<r)
{
mid=(l+r)/2;
if (dx[mid]<=x)
l=mid+1;
else
r=mid;
}
if (dx[l]<=x)
++l;
return d[l][0]*x+d[l][1];
}
void Init() //zhixian
{
int I,i,j,k,l=0;
long long K,B;
fo(I,1,tot)
{
i=C[I];
l2[i]=l+1;
T=0;
if (i>n)
{
T=1;
c[1]=i;
j=fa[i][0];
while (j && !bz[j])
{
c[++T]=j;
j=fa[j][0];
}
}
else
{
j=fa[i][0];
while (j && !bz[j])
{
c[++T]=j;
j=fa[j][0];
}
}
fd(j,T,1)
{
if (l2[i]>l)
{
++l;
d[l][0]=v[c[j]];
d[l][1]=sum[c[j]]*v[c[j]];
}
else
{
K=v[c[j]];
B=sum[c[j]]*v[c[j]];
while (l2[i]<l && dx[l-1]*K+B>=dx[l-1]*d[l][0]+d[l][1])
--l;
if (d[l][0]!=K)
{
++l;
d[l][0]=K;
d[l][1]=B;
dx[l-1]=(double)(d[l][1]-d[l-1][1])/(d[l-1][0]-d[l][0]);
}
}
}
r2[i]=l;
ANS[i]=find(i,0);
}
}
void work(int t)
{
while (t)
{
X[t]+=S;
ANS[t]=find(t,X[t]);
t=fa2[t];
}
}
void find()
{
int i;
fo(i,1,tot)
ans[A[I].id]=max(ans[A[I].id],ANS[C[i]]);
}
void Build()
{
int i,T,t2;
t2=1;
d2[1][0]=N;
d2[1][1]=0;
while (t2)
{
T=t2;
if (!d2[t2][1])
sum[d2[t2][0]]=w[d2[t2][0]];
if (d2[t2][1]<=1)
{
if (son[d2[t2][0]][d2[t2][1]])
{
++t2;
d2[t2][0]=son[d2[T][0]][d2[T][1]];
d2[t2][1]=0;
}
++d2[T][1];
}
else
{
if (!Bz[d2[t2][0]])
Ans=max(Ans,sum[d2[t2][0]]*v[d2[t2][0]]);
if (t2>1)
sum[d2[t2-1][0]]+=sum[d2[t2][0]];
--t2;
}
}
}
int main()
{
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
init();
N=n+n-1;
j=0;
dfs();
fo(i,1,Q)
scanf("%d%d",&A[i].x,&A[i].s),A[i].id=i;
for (L=1; L<=Q; L+=B)
{
Ans=0;
tot=0;
T=0;
R=min(L+B-1,Q);
build();
dfs2();
Init();
fo(I,L,R)
{
ans[A[I].id]=Ans;
S=A[I].s-w[A[I].x];
work(A[I].x);
find();
w[A[I].x]=A[I].s;
}
Build();
fo(i,1,tot)
bz[C[i]]=0,X[C[i]]=0;
}
fo(i,1,Q)
printf("%lld
",ans[i]);
fclose(stdin);
fclose(stdout);
return 0;
}