6441. 【GDOI2020模拟01.17】小 ω 维护序列

Description

Input

Output
输出到标准输出流中。
若干行，对于每个操作 1 和操作 5，输出一个数表示答案。

Sample Input
Sample Input1
5 8
1 2 3 2 1
1 1 3
5 1 5
2 2 4
1 2 4
3 3
4 0 5
1 1 2
1 1 5

Sample Input2
10 15
5 4 3 5 4 1 5 4 3 1
2 8 580347
4 6 503576
1 2 5
5 8 11
1 2 6
4 7 565239
3 6
3 11
3 3
2 9 674360
1 1 6
2 2 589693
4 5 236488
1 8 9
5 2 7

Sample Output
Sample Output1
6
3
24
0
78

【样例 1 解释】
操作 1，第 1 个到第 3 个元素之间不同的元素排序后得到 S = {1, 2, 3}，故答案为 1 × 2 × 3 = 6。
操作 2，第 1 个到第 5 个元素之间的不同元素有 S = {1, 2, 3}，故答案为 |S| = 3。
操作 3，序列 A 变为 [1, 4, 3, 2, 1]。
操作 4，第 2 个到第 4 个元素之间不同的元素排序后得到 S = {2, 3, 4}，故答案为 2×3×4 = 24。
操作 5，序列 A 变为 [1, 4, 2, 1]。
操作 6，序列 A 变为 [5, 1, 4, 2, 1]。
操作 7，第 1 个到第 2 个元素之间不同的元素排序后得到 S = {1, 5}，故答案为 0。
操作 8，第 1 个到第 5 个元素之间不同的元素排序后得到 S = {1, 2, 4, 5}，故答案为 1 × 2 × 4 +1 × 2 × 5 + 1 × 4 × 5 + 2 × 4 × 5 = 78。

Sample Output2
60
4
107
788510349
0
6

Data Constraint

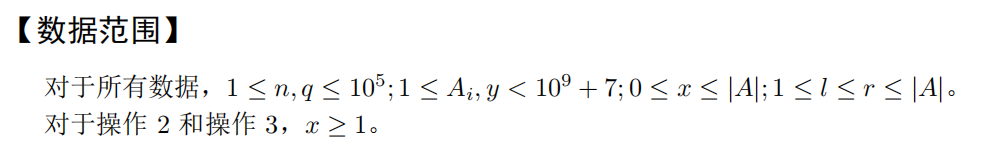
【子任务】
• 子任务 1（10 pts）：保证 n, q ≤ 100。
• 子任务 2（10 pts）：保证 q × n ≤ 2 × 10^7。
• 子任务 3（5 pts）：保证只有操作 5。
• 子任务 4（10 pts）：保证只有操作 1。
• 子任务 5（15 pts）：保证只有操作 2 和 5。
• 子任务 6（15 pts）：保证只有操作 1、2 和 5。
• 子任务 7（5 pts）：保证只有操作 2、3 和 4。
• 子任务 8（10 pts）：保证 n, q ≤ 50000。
• 子任务 9（20 pts）：没有额外限制。

题解

lj大数据结构题

把询问1拆成一次方、二次方、三次方和，询问5则是零次方和

没有34就是动态区间数颜色

求出每个数a[i]在其权值上的前驱ls[i]，把(ls[i],a[i])丢到平面上，这个可以用map套set

一次询问就是询问(1~L-1,L~R)的矩形，修改即把原先的点在原权值中删掉以及修改其后继（-1，+1），再修改其在新的权值中的后继，离线cdq即可

离线删除插入是经典套路，用平衡树求出每次操作所对应的最终序列位置

对于一次删除，不需要把它删掉，只需要把其size清0，然后在插入时通过平衡树二分找到对应点插入

所有的操作都需要在做到它时找到对应的树上节点（方便最后重标号）

最后再遍历一遍平衡树即可得到新的标号，把每次操作对应到新的序列

于是就可以把原先的插入删除变成修改操作，做法同上

code

6.4K

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <map>
#include <set>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define add(a,b) a=((a)+(b))%1000000007
#define low(x) ((x)&-(x))
#define mod 1000000007
#define file
using namespace std;

struct type{
	int tp,x,y;
} q[100001];
struct Type{
	int x,y;
	long long tp,s; //tp=1或-1时为修改(s=a值)，=0为询问(s=1或-1)
	int id,Id;
} b[700001];
int tr[200001][3]; //splay
long long Tr[200002][4]; //树状数组
int fa[200001];
bool bz[200001];
int a[100001];
long long c[200001];
int num[100001];
int ls[100001];
long long ans[100001][4];
bool Bz[200002];
int d[200002];
map<int,set<int> > hs;
map<int,set<int> > :: iterator I;
set<int> :: iterator I2;
int n,Q,i,j,k,l,len,root,Len,tot;
long long f0,f1,f2,f3;
const long long S=166666668; // 1/6

bool cmp(Type a,Type b)
{
	return a.x<b.x || a.x==b.x && a.tp!=0 && b.tp==0;
}

void look()
{
	int i;
	
	fo(i,1,len)
	cout<<i<<": fa:"<<fa[i]<<" son:"<<tr[i][0]<<" "<<tr[i][1]<<" size:"<<tr[i][2]<<endl;
	cout<<endl;
}

void look2()
{
	int i;
	
	fo(i,1,Len)
	cout<<"type:"<<b[i].tp<<" "<<b[i].s<<" x,y:"<<b[i].x<<" "<<b[i].y<<" id:"<<b[i].id<<endl;
	cout<<endl;
}

//splay ↓

void up(int t)
{
	tr[t][2]=bz[t]+tr[tr[t][0]][2]+tr[tr[t][1]][2];
}

void mt(int ls,int l,int r,int tp)
{
	int mid=(l+r)/2;
	
	if (ls)
	fa[mid]=ls,tr[ls][tp]=mid;
	
	if (l<=mid-1) mt(mid,l,mid-1,0);
	if (mid+1<=r) mt(mid,mid+1,r,1);
	
	up(mid);
}

void rot(int t)
{
	int Fa=fa[t],Fa2=fa[Fa],x=tr[Fa][1]==t,x2=tr[Fa2][1]==Fa,son=tr[t][x^1];
	
	if (Fa==root) root=t;
	
	fa[Fa]=t;tr[Fa2][x2]=t;
	fa[t]=Fa2;tr[Fa][x]=son;
	fa[son]=Fa;tr[t][x^1]=Fa;
	
	up(Fa);up(t);
}

void splay(int t,int x)
{
	while (fa[t]!=x)
	{
		int Fa=fa[t];
		
		if (fa[Fa]!=x)
		{
			int Fa2=fa[Fa];
			
			if ((tr[Fa2][0]==Fa)^(tr[Fa][0]==t))
			rot(t),rot(t);
			else
			rot(Fa),rot(t);
		}
		else
		rot(t);
	}
}

void New(int t,int x)
{
	int i;
	
	tr[t][x]=++len;
	fa[len]=t;
	
	i=len;
	while (i)
	++tr[i][2],i=fa[i];
	
	splay(len,0);
}

int find(int t)
{
	int i=root;
	
	while (1)
	{
		if (t<=tr[tr[i][0]][2])
		i=tr[i][0];
		else
		if (tr[tr[i][0]][2]+1==t && bz[i])
		return i;
		else
		t-=tr[tr[i][0]][2]+bz[i],i=tr[i][1];
	}
}

void ins(int t)
{
	int x,y;
	
	if (!t)
	{
		x=root;
		while (tr[x][0])
		x=tr[x][0];
		
		New(x,0);
	}
	else
	if (t==tr[root][2])
	{
		x=root;
		while (tr[x][1])
		x=tr[x][1];
		
		New(x,1);
	}
	else
	{
		x=find(t);y=find(t+1);
		
		splay(x,0);splay(y,x);
		
		while (tr[y][0]) //可能y的左儿子被删了(即还存在)
		y=tr[y][0];
		New(y,0);
	}
}

void del(int t) //不真正删掉
{
	int x=find(t);
	l=x;
	
	bz[x]=0;
	while (x)
	--tr[x][2],x=fa[x];
}

void dfs(int t) //遍历求出每个节点的新编号
{
	if (tr[t][0]) dfs(tr[t][0]);
	num[t]=++j;
	if (tr[t][1]) dfs(tr[t][1]);
}

//splay ↑

int hs_nxt(int t,int x) //前驱
{
	I=hs.find(t);
	if (I==hs.end())
	return 0;
	
	I2=(I->second).upper_bound(x);
	if (I2==(I->second).end())
	return 0;
	
	return *I2;
}

int hs_pre(int t,int x) //后继
{
	I=hs.find(t);
	if (I==hs.end())
	return 0;
	
	I2=(I->second).lower_bound(x);
	if (I2==(I->second).begin())
	return 0;
	
	--I2;
	return *I2;
}

void hs_ins(int t,int x)
{
	I=hs.find(t);
	if (I==hs.end())
	{
		hs.insert(pair<int,set<int>>(t,{}));
		I=hs.find(t);
	}
	
	(I->second).insert(x);
}

void hs_del(int t,int x)
{
	I=hs.find(t);
	(I->second).erase(x);
}

void work_inc(int t,int s) //插入
{
	int l=hs_pre(s,t),r=hs_nxt(s,t);
	
	b[++Len]={l,t,1,s,0};
	if (r)
	b[++Len]={l,r,-1,c[r],0},b[++Len]={t,r,1,c[r],0},ls[r]=t;
	
	hs_ins(s,t);
	c[t]=s;ls[t]=l;
}

void work_dec(int t) //清零
{
	int l=hs_pre(c[t],t),r=hs_nxt(c[t],t);
	
	b[++Len]={ls[t],t,-1,c[t],0};
	if (r)
	b[++Len]={t,r,-1,c[r],0},b[++Len]={l,r,1,c[r],0},ls[r]=l;
	
	hs_del(c[t],t);
	c[t]=ls[t]=0;
}

void t_change(int t,long long tp,long long s) //树状数组
{
	long long s0=tp,s1=tp*s,s2=tp*s*s%mod,s3=tp*s*s%mod*s%mod;
	int i;
	
	while (t<=len+1)
	{
		if (!Bz[t]) Bz[t]=1,d[++tot]=t;
		
		Tr[t][0]+=s0,add(Tr[t][1],s1),add(Tr[t][2],s2),add(Tr[t][3],s3);
		t+=low(t);
	}
}

void t_find(int t)
{
	int i;
	f0=f1=f2=f3=0;
	
	while (t)
	{
		f0+=Tr[t][0],add(f1,Tr[t][1]),add(f2,Tr[t][2]),add(f3,Tr[t][3]);
		t-=low(t);
	}
}

void work(int l,int r)
{
	int mid=(l+r)/2;
	
	if (l==r) return;
	
	work(l,mid);
	work(mid+1,r);
	
	stable_sort(b+l,b+r+1,cmp);
	
	tot=0;
	
	fo(i,l,r)
	if (b[i].tp!=0 && b[i].Id<=mid)
	t_change(b[i].y,b[i].tp,b[i].s);
	else
	if (b[i].tp==0 && b[i].Id>mid)
	{
		t_find(b[i].y);
		ans[b[i].id][0]+=f0*b[i].s,add(ans[b[i].id][1],f1*b[i].s),add(ans[b[i].id][2],f2*b[i].s),add(ans[b[i].id][3],f3*b[i].s);
	}
	
	fo(i,1,tot) Bz[d[i]]=0,Tr[d[i]][0]=Tr[d[i]][1]=Tr[d[i]][2]=Tr[d[i]][3]=0;
}

int main()
{
	freopen("maintain.in","r",stdin);
	#ifdef file
	freopen("maintain.out","w",stdout);
	#endif
	
	memset(bz,1,sizeof(bz));
	
	scanf("%d%d",&n,&Q);
	fo(i,1,n)
	scanf("%d",&a[i]);
	
	mt(0,1,n,0);
	len=n;root=(1+n)/2;
	
//	--- 重标号
	
	fo(i,1,Q)
	{
		scanf("%d%d",&q[i].tp,&q[i].x);
		if (q[i].tp!=3)
		scanf("%d",&q[i].y);
		
		switch (q[i].tp) //指向树中节点
		{
			case 1:{q[i].x=find(q[i].x);q[i].y=find(q[i].y);break;}
			case 2:{q[i].x=find(q[i].x);break;}
			case 3:{del(q[i].x);q[i].x=l;break;}
			case 4:{ins(q[i].x);q[i].x=len;break;}
			case 5:{q[i].x=find(q[i].x);q[i].y=find(q[i].y);break;}
		}
	}
	
	j=0;dfs(root);
	
	fo(i,1,Q)
	{
		q[i].x=num[q[i].x];
		if (q[i].tp==1 || q[i].tp==5)
		q[i].y=num[q[i].y];
	}
	
//	--- cdq
	
	fo(i,1,n)
	{
		hs_ins(a[i],num[i]);
		ls[num[i]]=hs_pre(a[i],num[i]);
		
		c[num[i]]=a[i];
		b[++Len]={ls[num[i]],num[i],1,a[i],0};
	}
	
	fo(i,1,Q)
	{
		switch (q[i].tp)
		{
			case 2:{work_dec(q[i].x);work_inc(q[i].x,q[i].y);break;}
			case 3:{work_dec(q[i].x);break;}
			case 4:{work_inc(q[i].x,q[i].y);break;}
			default:{b[++Len]={q[i].x-1,q[i].x-1,0,-1,i};b[++Len]={q[i].x-1,q[i].y,0,1,i};break;}//1 or 5
		}
	}
	fo(i,1,Len) ++b[i].x,++b[i].y,b[i].Id=i; //坐标可能为0
	
	work(1,Len);
	
//	---
	
	fo(i,1,Q)
	if (q[i].tp==1)
	printf("%lld
",((ans[i][1]*ans[i][1]%mod*ans[i][1]+2ll*ans[i][3]-3ll*ans[i][2]*ans[i][1])%mod+mod)%mod*S%mod);
	else
	if (q[i].tp==5)
	printf("%lld
",ans[i][0]);
	
	fclose(stdin);
	fclose(stdout);
	
	return 0;
}