题目描述

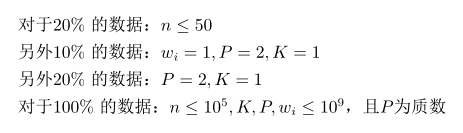
题解
设%P>0为1,=0为0,则一个不合法的三元组必然存在有两条路01相同,也就是两条路01不同
点分治求出每个点向外&从外到内的不同01的路径条数(从每个点分中心向下走时统计兄弟子树中的点),之后随便算算即可,要考虑uvt中有两个相等的情况
注意p为质数,所以kx≠0(mod p),所以可以把分治中心设为w*k1,向前乘k向后乘k^-1,使得左右两边相等即可
不要用vector
code
#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define max(a,b) (a>b?a:b)
#define LEN 20000007
#define ll long long
#define file
using namespace std;
int a[200001][2],ls[100001],size[100001],d1[100001],d2[100001],hs[2][LEN][2],D[2][100001],N,n,p,i,j,k,l,len,x,y,find1,find2,sum,tot[2];
ll w[100001],ans,s1,s2,f[100001][2],g[100001][2],K,K2,k2,k22; //f=in g=out
bool bz[100001],BZ[2][LEN],Bz;
ll qpower(ll a,int b)
{
ll ans=1;
while (b)
{
if (b&1) ans=ans*a%p;
a=a*a%p;
b>>=1;
}
return ans;
}
void New(int x,int y)
{
++len;
a[len][0]=y;
a[len][1]=ls[x];
ls[x]=len;
}
int hash(int T,int t,int s)
{
int i=t%LEN,S;
while (BZ[T][i] && hs[T][i][0]!=t)
i=(i+1)%LEN;
S=hs[T][i][1];
if (!BZ[T][i])
{
if (s)
{
hs[T][i][0]=t;
hs[T][i][1]+=s;
BZ[T][i]=1;
D[T][++tot[T]]=i;
}
}
else
{
hs[T][i][0]=t;
hs[T][i][1]+=s;
}
return S;
}
void dfs(int Fa,int t)
{
int i,mx=0;
size[t]=1;
for (i=ls[t]; i; i=a[i][1])
if (a[i][0]!=Fa && !bz[a[i][0]])
{
dfs(t,a[i][0]);
size[t]+=size[a[i][0]];
mx=max(mx,size[a[i][0]]);
}
mx=max(mx,N-size[t]);
if (mx<find1)
find1=mx,find2=t;
}
void dfs2(int Fa,int t,ll sum1,ll sum2,ll s1,ll s2,int S)
{
int i;
if (Bz) d1[t]=sum1,d2[t]=sum2;
else
sum1=d1[t],sum2=d2[t];
hash(0,sum1,S),hash(1,sum2,S);
sum+=S;
for (i=ls[t]; i; i=a[i][1])
if (a[i][0]!=Fa && !bz[a[i][0]])
{
if (Bz)
dfs2(t,a[i][0],(sum1+s1*w[a[i][0]])%p,(sum2+s2*w[a[i][0]])%p,s1*K%p,s2*K2%p,S);
else
dfs2(t,a[i][0],0,0,0,0,S);
}
}
void dfs3(int Fa,int t,int S)
{
ll sum1=d1[t],sum2=d2[t];
int i,s;
s=hash(1,(p-sum1)%p,0),f[t][0]+=s,f[t][1]+=sum-s;
s=hash(0,(p-sum2)%p,0),g[t][0]+=s,g[t][1]+=sum-s;
for (i=ls[t]; i; i=a[i][1])
if (a[i][0]!=Fa && !bz[a[i][0]])
dfs3(t,a[i][0],S);
}
void work(int n,int t)
{
int i,s;
N=n;
find1=n+1;
dfs(0,t);
t=find2;
bz[t]=1;
Bz=1;
dfs2(0,t,w[t],0,K,K2,1);
Bz=0;
s=hash(1,(p-w[t])%p,0);f[t][0]+=s-(w[t]==0);f[t][1]+=(sum-1)-(s-(w[t]==0));
s=hash(0,0,0);g[t][0]+=s-(w[t]==0);g[t][1]+=(sum-1)-(s-(w[t]==0));
for (i=ls[t]; i; i=a[i][1])
if (!bz[a[i][0]])
{
dfs2(t,a[i][0],0,0,0,0,-1);
dfs3(t,a[i][0],-1);
dfs2(t,a[i][0],0,0,0,0,1);
}
dfs2(0,t,w[t],0,K,K2,-1);
fo(i,1,tot[0]) hs[0][D[0][i]][0]=hs[0][D[0][i]][1]=BZ[0][D[0][i]]=0;
fo(i,1,tot[1]) hs[1][D[1][i]][0]=hs[1][D[1][i]][1]=BZ[1][D[1][i]]=0;
tot[0]=tot[1]=0;
for (i=ls[t]; i; i=a[i][1])
if (!bz[a[i][0]])
{
if (size[t]>size[a[i][0]])
work(size[a[i][0]],a[i][0]);
else
work(n-size[t],a[i][0]);
}
bz[t]=0;
}
int main()
{
freopen("tree.in","r",stdin);
#ifdef file
freopen("tree.out","w",stdout);
#endif
scanf("%d%lld%d",&n,&K,&p),K%=p;K2=qpower(K,p-2);k2=K*K%p,k22=K2*K2%p;
fo(i,1,n)
scanf("%lld",&w[i]),w[i]=w[i]*K%p;
fo(i,2,n)
scanf("%d%d",&x,&y),New(x,y),New(y,x);
work(n,1);
fo(i,1,n)
ans+=(g[i][0]*g[i][1])*2+(f[i][0]*g[i][1]+f[i][1]*g[i][0])+(f[i][0]*f[i][1])*2+(g[i][!w[i]]+g[i][!w[i]])+(g[i][!w[i]]+f[i][!w[i]])+(f[i][!w[i]]+f[i][!w[i]]);
printf("%lld
",1ll*n*n*n-ans/2);
fclose(stdin);
fclose(stdout);
return 0;
}