loj#6693. 「MtOI2019」幽灵乐团

题目描述

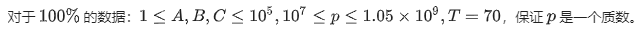
题解

简单数论题

式子太多了所以简略说明

type=-1

看错题的产物

求(sum_{i=1}^{A} sum_{j=1}^{B} sum_{k=1}^{C} (frac{gcd(i,j)}{lcm(i,k)}))

以下定义((a,b)=gcd(a,b))

(sum_{i=1}^{A} frac{1}{i}sum_{j=1}^{B} (i,j)sum_{k=1}^{C} (i,k)frac{1}{k})

最后面的东西应该可以枚举约数+反演+分块解决

type=0

因为是Π所以显然可以拆开上下两部分算

化一下变成求①(prod_i prod_j prod_k i^{f(type)})和②(prod_i prod_j prod_k (i,j)^{f(type)})

①预处理做到O(log)，②变成

((prod_{d>=1}prod_eprod_{d^e|i} prod_{d^e|j} d)^C)，直接枚举d^e整数分块计算

type=1

①预处理做到O(log)，②变成

((prod_{d>=1}prod_eprod_{d^e|i} prod_{d^e|j} d^{...})^{(C+1)C/2})

设(s1=left lfloor frac{B}{d^e} ight floor)，(s2=left lfloor frac{C}{d^e} ight floor)，…处是(d^{2e}(s1+1)s1/2*(s2+1)s2/2)

整数分块计算

type=2

①式：

(prod_i prod_j prod_k i^{(i,j,k)})

(=prod_d prod_{d|i} prod_{d|j} prod_{d|k} i^{varphi(d)})

把d提出来之后整数分块

②式：

(prod_i prod_j prod_k (i,j)^{(i,j,k)})

(=prod_d prod_{d|i} prod_{d|j} prod_{d|k} (i,j)^{varphi(d)})

把d提出来之后变成type=0的问题，整数分块

共计4个整数分块，时间复杂度约为O(Tnlog)

code

#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define min(a,b) (a<b?a:b)
#define ll long long
//#define file
using namespace std;

ll phi[100001],Phi[100001],sum[100001],Sum[100001],D[100001],D2[100001],Dd[100001],Dd2[100001],Dp[100001],Dp2[100001],A,B,C,two;
int p[100001],T,n,i,j,k,l,mod,Mod,len;
bool f[100001];

ll qpower(ll a,int b,int mod) {ll ans=1; while (b) {if (b&1) ans=ans*a%mod;a=a*a%mod;b>>=1;} return ans;}
void init()
{
	int i,j;
	ll d,s;
	
	sum[0]=Sum[0]=1;
	fo(i,1,100000) sum[i]=sum[i-1]*i%mod,Sum[i]=Sum[i-1]*qpower(i,i,mod)%mod,D[i]=Dd[i]=Dp[i]=1;
	f[1]=phi[1]=1;
	fo(i,2,100000)
	{
		if (!f[i]) p[++len]=i,phi[i]=i-1;
		
		fo(j,1,len)
		if (1ll*i*p[j]<=100000)
		{
			f[i*p[j]]=1;phi[i*p[j]]=phi[i]*p[j];
			if (!(i%p[j])) break;
			phi[i*p[j]]=phi[i*p[j]]/p[j]*(p[j]-1);
		}
		else break;
	}
	
	D[0]=D2[0]=Dd[0]=Dd2[0]=Dp[0]=Dp2[0]=1;
	fo(d,1,100000)
	{
		Phi[d]=Phi[d-1]+phi[d];
		if (!f[d])
		{
			for (s=d; s<=100000; s*=d)
			D[s]=d,Dd[s]=qpower(d,s*s%(mod-1),mod);
		}
		Dp[d]=qpower(d,phi[d],mod);
	}
	fo(i,1,100000) D[i]=D[i]*D[i-1]%mod,D2[i]=qpower(D[i],Mod,mod),Dd[i]=Dd[i]*Dd[i-1]%mod,Dd2[i]=qpower(Dd[i],Mod,mod),Dp[i]=Dp[i]*Dp[i-1]%mod,Dp2[i]=qpower(Dp[i],Mod,mod);
}

namespace task1{
	ll js1(ll A,ll B,ll C) {return qpower(sum[A],(B*C)%(mod-1),mod);}
	ll js2(ll A,ll B,ll C)
	{
		int d,e,i,j,k=min(A,B);
		ll ans=1,s1,s2,s;
		
		d=1;
		while (d<=k)
		{
			s1=A/d,s2=B/d,s=(s1*s2)%(mod-1);
			i=A/s1,j=B/s2;
			ans=ans*qpower(D[min(min(i,j),k)]*D2[d-1]%mod,s,mod)%mod;
			d=min(i,j)+1;
		}
		return qpower(ans,C,mod);
	}
	ll work(ll A,ll B,ll C) {return (js1(A,B,C)*js1(B,A,C)%mod*qpower(js2(A,B,C)*js2(A,C,B)%mod,Mod,mod)%mod+mod)%mod;}
}

namespace task2{
	ll js1(ll A,ll B,ll C) {return qpower(Sum[A],(((1+B)*B/2%(mod-1))*((1+C)*C/2%(mod-1)))%(mod-1),mod);}
	ll js2(ll A,ll B,ll C)
	{
		int d,e,i,j,k=min(A,B);
		ll ans=1,s1,s2,s;
		
		d=1;
		while (d<=k)
		{
			s1=A/d,s2=B/d,s=((((s1+1)*s1/2)%(mod-1))*(((s2+1)*s2/2)%(mod-1)))%(mod-1);
			i=A/s1,j=B/s2;
			ans=ans*qpower(Dd[min(min(i,j),k)]*Dd2[d-1]%mod,s,mod)%mod;
			d=min(i,j)+1;
		}
		return qpower(ans,(C+1)*C/2%(mod-1),mod);
	}
	ll work(ll A,ll B,ll C) {return (js1(A,B,C)*js1(B,A,C)%mod*qpower(js2(A,B,C)*js2(A,C,B)%mod,Mod,mod)%mod+mod)%mod;}
}

namespace task3{
	ll js1(ll A,ll B,ll C)
	{
		ll ans=1,s1,s2,s3;
		int d,i,j,k,l,D;
		
		l=min(A,min(B,C));d=1;
		while (d<=l)
		{
			s1=A/d,s2=B/d,s3=C/d;
			i=A/s1,j=B/s2,k=C/s3;D=min(min(i,j),k);
			ans=ans*qpower(Dp[min(D,l)]*Dp2[d-1]%mod,s1*s2%(mod-1)*s3%(mod-1),mod)%mod*qpower(sum[s1],(Phi[D]-Phi[d-1])%(mod-1)*s2%(mod-1)*s3%(mod-1),mod)%mod;
			d=D+1;
		}
		return ans;
	}
	ll js2(ll A,ll B,ll C)
	{
		ll ans=1,s1,s2,s3,s;
		int d,i,j,k,l,D;
		
		l=min(A,min(B,C));d=1;
		while (d<=l)
		{
			if (d==1 || A/d!=A/(d-1) || B/d!=B/(d-1)) s=task1::js2(A/d,B/d,1);
			
			s1=A/d,s2=B/d,s3=C/d;
			i=A/s1,j=B/s2,k=C/s3;D=min(min(i,j),k);
			ans=ans*qpower(Dp[min(D,l)]*Dp2[d-1]%mod,s1*s2%(mod-1)*s3%(mod-1),mod)%mod*qpower(s,s3*((Phi[D]-Phi[d-1])%(mod-1))%(mod-1),mod)%mod;
			d=D+1;
		}
		return ans;
	}
	ll work(ll A,ll B,ll C) {return (js1(A,B,C)*js1(B,A,C)%mod*qpower(js2(A,B,C)*js2(A,C,B)%mod,Mod,mod)%mod+mod)%mod;}
}

int main()
{
	#ifdef file
	freopen("loj6693.in","r",stdin);
	#endif
	
	scanf("%d%d",&T,&mod);Mod=mod-2;two=(mod+1)/2;
	init();
	for (;T;--T)
	{
		scanf("%lld%lld%lld",&A,&B,&C);
		printf("%lld %lld %lld
",task1::work(A,B,C),task2::work(A,B,C),task3::work(A,B,C));
	}
	
	fclose(stdin);
	fclose(stdout);
	return 0;
}