CF1444D. Rectangular Polyline

题目大意

给出n条水平线段和m条竖直线段，将其组合成一个多边形满足封闭且边不相交，构造方案

Σn+m<=1e3,len<=1e3

题解

被C搞死了

显然可以类似

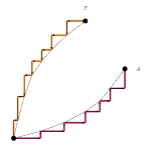
这样构造，红色的按照水平大->小、竖直小->大放，黄色的反之

dp设f[i,j]表示放了前i和为j，bitset优化，最后逆推求出方案

问题是这样没法保证水平和竖直的个数相等，因此再把上面的补成这样

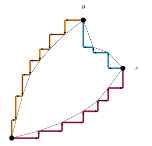
把蓝色段水平的分给一边，竖直的分给另一边即可使其个数相等，构造方法类似

code

#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define ll long long
//#define file
using namespace std;

int a[1001],b[1001],d[2][2][1001],D[2][1001],T,n,m,i,j,k,l,t[2][2],I,s1,s2,x,y,t2[2];
bitset<1000001> f[1001];
bool bz,Bz;

void work(int *a,int I,int s)
{
	int i,j,k,l;
	fo(i,1,n) f[i]=f[i-1]|(f[i-1]<<a[i]);
	
	if (f[n][s])
	{
		fd(i,n,1)
		if (s>=a[i] && f[i-1][s-a[i]])
		s-=a[i],d[I][0][++t[I][0]]=a[i];
		else d[I][1][++t[I][1]]=a[i];
	}
	else bz=1;
}

void Write()
{
	if (Bz)
	printf("%d %d
",y,x);
	else
	printf("%d %d
",x,y);
}

int main()
{
	#ifdef file
	freopen("CF1444D.in","r",stdin);
	#endif
	
	scanf("%d",&T),f[0][0]=1;
	for (;T;--T)
	{
		s1=s2=bz=Bz=t[0][0]=t[0][1]=t[1][0]=t[1][1]=0;
		scanf("%d",&n);fo(i,1,n) scanf("%d",&a[i]),s1+=a[i];
		scanf("%d",&m);fo(i,1,m) scanf("%d",&b[i]),s2+=b[i];
		sort(a+1,a+n+1),sort(b+1,b+n+1);
		
		if ((s1&1) || (s2&1) || n!=m) {printf("No
");continue;}
		s1>>=1,s2>>=1;
		work(a,0,s1);
		work(b,1,s2);
		if (bz) {printf("No
");continue;}
		
		printf("Yes
");
		I=Bz=t[0][0]>t[1][0];
		
		x=y=t2[0]=t2[1]=0;
		fo(i,1,t[I][0]) D[0][++t2[0]]=d[I][0][i];
		fo(i,1,t[I][1]) D[0][++t2[0]]=-d[I][1][i];
		fd(i,t[I^1][0],1) D[1][++t2[1]]=d[I^1][0][i];
		fd(i,t[I^1][1],1) D[1][++t2[1]]=-d[I^1][1][i];
		fo(i,1,n)
		{
			x+=D[0][i],Write();
			y+=D[1][i],Write();
		}
	}
	
	fclose(stdin);
	fclose(stdout);
	return 0;
}