间间断断的将9种排序实现,并且将其以博客笔记的形式记录下来;现在就该来综合的分析这九种排序,让我们先来看看其算法复杂度和稳定性的分析结果:
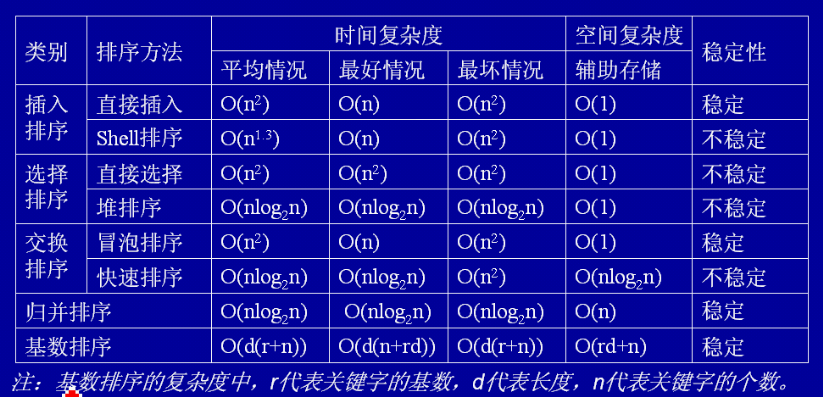
算法复杂度以及稳定性分析
| 算法名称 | 平均时间 | 辅助空间 | 稳定性 |
| 冒泡排序 | O(n2) | O(1) | 是 |
| 选择排序 | O(n2) | O(1) | 否 |
| 插入排序 | O(n2) | O(1) | 是 |
| 自底向上归并排序 | O(nlog2n) | O(n) | 是 |
| 自顶向下归并排序 | O(nlog2n) | O(n) | 是 |
| 快速排序 | O(nlog2n) | O(n) | 否 |
| 堆排序 | O(nlog2n) | O(1) | 否 |
| 基数排序 | O(dn) | O(rn) | 是 |
| 希尔排序 | O(1) | 否 |
排序的时间效率比较
下图表名了各种算法在不同数据规模下,完成排序所消耗的时间(毫秒为单位),从表中可以显然看出O(n2)的排序算法比O(nlog2n)的算法 时间多出几百上千倍,而且随着数据数据规模增大时间比也会随着增大;因为排序的数据采用随机数,顺序将被打乱,快速排序算法优于其他排序算法!
| 算法名称 | 1万 | 2万 | 3万 | 4万 | 5万 | 6万 | 7万 | 8万 | 9万 | 10万 |
| 冒泡排序 | 1442 | 5497 | 12206 | 21861 | 34017 | 49148 | 67394 | 88880 | 111939 | 139071 |
| 选择排序 | 199 | 816 | 1790 | 3254 | 5062 | 7166 | 9645 | 12636 | 16102 | 19643 |
| 插入排序 | 178 | 717 | 1628 | 2882 | 4458 | 6446 | 8822 | 11649 | 14547 | 17914 |
| 自底向上归并排序 | 3 | 6 | 9 | 12 | 15 | 18 | 22 | 26 | 28 | 33 |
| 自顶向下归并排序 | 3 | 7 | 11 | 15 | 18 | 23 | 27 | 31 | 36 | 40 |
| 快速排序 | 2 | 5 | 8 | 11 | 14 | 18 | 21 | 25 | 29 | 32 |
| 堆排序 | 3 | 7 | 12 | 16 | 19 | 23 | 26 | 30 | 34 | 37 |
| 基数排序 | 9 | 21 | 30 | 40 | 49 | 59 | 66 | 75 | 90 | 98 |
| 希尔排序 | 3 | 8 | 11 | 15 | 24 | 24 | 29 | 35 | 40 | 41 |
下面采用图表形式将数据直观展示出来(将O(n2)的算法和O(nlog2n)算法分开,因为完全不是一个数量级的):


上图显示快排速度和自底向上归并排序奇虎相当,接下来是堆排序、希尔排序;出乎意料的是基数排序,号称O(dn)的基数排序却不是那么靠前,个人觉得和冒泡排序速度慢的原因相同,赋值操作太多,降低了时间效率。
修正更新:
2012-9-13
【1】 修改归并排序的代码,并重新生成测试结果
【2】 上传九种排序的实现代码(下载地址:http://download.csdn.net/detail/cjf_iceking/4567202)
附: