记数排序

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

int find_max(int arr[],int len)
{
   int max;
   int i;
   max = arr[0];
   for(i = 0 ; i < len;i++)
   {
          if( arr[i] > max)
              max = arr[i];      
   }
   return max;
    
}

int count_sort(int arr[],int max,int len)
{
      int* mid;
      int i;
      mid = (int*)malloc(sizeof(int)*(max+1));
      for(i = 0; i <= max ; i++){
           mid[i] = 0;      
      }
      for(i = 0; i <= len ; i++){
          mid[arr[i]]++;      
      }
      int z = 0;    
      for(i = 0; i<= max; i++){
            while(mid[i]-- > 0){
               arr[z++] = i;               
            }
      }
      free(mid);
}

int main()
{
   int s[10];
   int t,i;
   printf("input a int array:");
   for(i=0;i<10;i++){
        scanf("%d",&t);
        s[i] = t;
    }
   int max = find_max(s,10);
   printf("max = %d\n",max);
   count_sort(s,max,10);
   printf("after sort:\n");
    for(i=0;i<10;i++){
       printf("%d",s[i]);
    }
   system("pause");
   return 0;    
}

网上的资料：

计数排序是一种算法复杂度 O(n) 的排序方法，适合于小范围集合的排序。比如100万学生参加高考，我们想对这100万学生的数学成绩（假设分数为0到100）做个排序。我们如何设计一个最高效的排序算法。本文不光给出计数排序算法的传统写法，还将一步步深入讨论算法的优化，直到时间复杂度和空间复杂度最优。

计数排序是一个类似于桶排序的排序算法，其优势是对已知数量范围的数组进行排序。它创建一个长度为这个数据范围的数组C，C中每个元素记录要排序数组中对应记录的出现个数。这个算法于1954年由 Harold H. Seward 提出。

下面以示例来说明这个算法

假设要排序的数组为 A = {1,0,3,1,0,1,1}

这里最大值为3，最小值为0，那么我们创建一个数组C，长度为4.

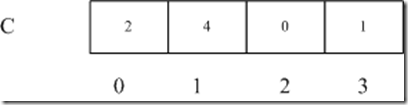
然后一趟扫描数组A，得到A中各个元素的总数，并保持到数组C的对应单元中。

比如0 的出现次数为2次，则 C[0] = 2;1 的出现次数为4次，则C[1] = 4

由于C 是以A的元素为下标的，所以这样一做，A中的元素在C中自然就成为有序的了，这里我们可以知道 顺序为 0,1,3 (2 的计数为0)

然后我们把这个在C中的记录按每个元素的计数展开到输出数组B中，排序就完成了。

也就是 B[0] 到 B[1] 为0  B[2] 到 B[5] 为1 这样依此类推。

这种排序算法，依靠一个辅助数组来实现，不基于比较，算法复杂度为 O(n) ，但由于要一个辅助数组C，所以空间复杂度要大一些，由于计算机的内存有限，这种算法不适合范围很大的数的排序。

注：基于比较的排序算法的最佳平均时间复杂度为 O(nlogn)