已知特征(X=x_1)的样本呈现(Y=y_1)的特点,或者(Y=y_1)的样本有(X=x_1)的特征,如何计算干预X对Y的影响
Eg. 看快手视频喜欢评论的用户活跃程度更高,那引导用户去发表评论能让他们更活跃么?
建模特征应该如何选择,以及特征通过那些途径最终影响Y
Eg. 个人并不喜欢有啥放啥的建模方式,既增加模型不稳定性还会增加特征解释的难度。尤其在业务中我们跟多想知道的是不同特征影响Y的方式
如何解释数据分析中有违常理或者自相矛盾的结论?为什么把数据分组和整体计算会得到不同的结果?
Eg. 药物实验结果表明对高血压患者药物无效,对低血压患者药物也无效,但合起来对全部患者药物有效?
无法开展AB实验的时候,我们如何从观测数据中估计因果关系
Eg. 最常遇到这种问题的是社会学,医学实验,例如当兵经历对收入的影响,吸烟是否会得肺癌。但这也提醒我们有些成本高的AB实验其实是有可能从已有数据中找到近似答案的。
如果你在和数据打交道的过程中也碰到过以上的问题,那图灵奖得主Judea Pearl的The Book of WHY可能会帮你打开新世界的大门。因果推理方面我也是新人,这里只是抛出一些观点来和大家一起讨论。下面列举了因果推理和统计学本质的一些差异, 具体的理论我们在后面章节慢慢展开~
-
统计学解决的是P(Y|X),它更多是对观测的刻画。而因果推理旨在解决What-if问题,用Do-Caculus来表达就是P(Y|do(X)),既对X进行干预,对Y的影响。一个同事开玩笑说因果推理就像开启上帝之眼
-
统计学认为数据是一切,而因果推理坚持数据产生的过程是解释数据所必须的。想直观感受差异的可以看下这个 Toy Example
-
统计完全客观,而因果推理需要依赖基于经验等因素给出因果图(DAG)再进行分析计算。
作为序章最重要的是什么?吸引人眼球!所以本章通过5个数据分析中经典案例,看看当统计陷入两难,因果推理是如何变身奥特曼来打小怪兽的!
以下案例只为直观感受因果推理的现实意义,暂不考虑统计显著,小样本不置信等问题
Confounding Bias - Simpson Paradox
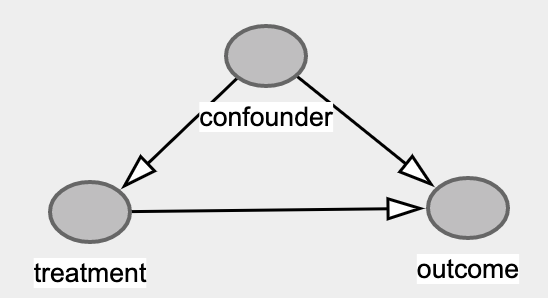
Confounding在数据分析中非常常见,既存在同时影响treatment和outcome的变量没有被控制,它是统计分析要控制变量的根本原因之一,是AB实验有效的背后逻辑,它也直接导致了(P(Y|X) eq p(Y|do(x)))。但往往Confounder的存在只有在分析结果严重不符合逻辑时才被人们想到。
离散Confounder - 案例1. 今天你吃药了么?
以下是一次观测性医学实验的结果,分别给出男性和女性在服/不服用药物后心脏病发作的概率。有趣的是这种药物既不能显著降低女性病发概率,也不能显著降低男性病发概率,但却能降低整体的病发概率,你是分析师请问这种药物有用么?
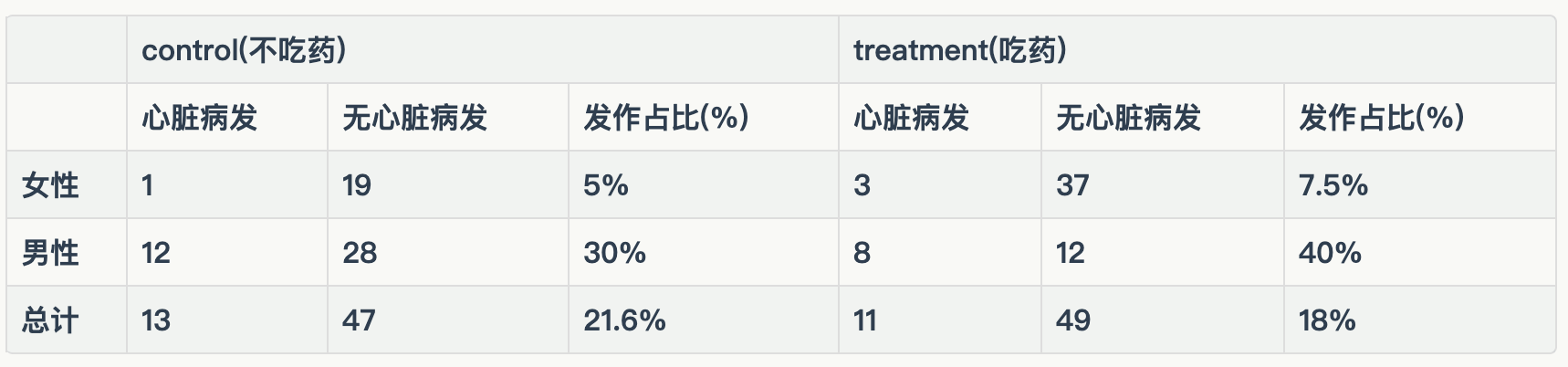
答案是NO,这种药物无效
这就是著名的Simpson Paradox。用上面的因果图(DAG)分析结论会变得显而易见。这里treatment是服药,outcome是心脏病发作的概率,而因为是观测性实验所以性别可能会成为confounder。注意这里我用的是可能。而验证这种可能性就要看性别是否同时影响treatment和outcome。先看treatment,女性是对照组20,实验组40,而男性是对照组40,实验组20。因此性别显著影响treatment的渗透率 -服药人群比例。再看outcome,同在对照组女性病发率是5%而男性是30%,因此性别同时影响outcome-病发概率。
因此衡量treatment(服药)对outcome(心脏病发作)的影响,我们需要控制confounder。这样总体的发病率计算如下:
对照组的整体效果变为 0.5 * 5% + 0.5 * 40% = 17.5%
实验组的整体效果变为 0.5 * 7.5% + 0.5 * 40% = 23.75%
这样整体就和男女分别的结论一致,服药并不能降低心脏病发概率。
连续Confounder - 案例2.运动导致高胆固醇?
在上面的例子中confounder是个离散变量男女。下面我们举个连续confounder的例子。研究目标是每周运动时间对胆固醇水平的影响。‘影响’在统计学中多数只能依赖于相关关系,于是我们画个散点图吧。
嗯?!运动时间越长,胆固醇水平越高!You What?! 这简直是厌恶运动,坚持生命在于静止的最好理由。
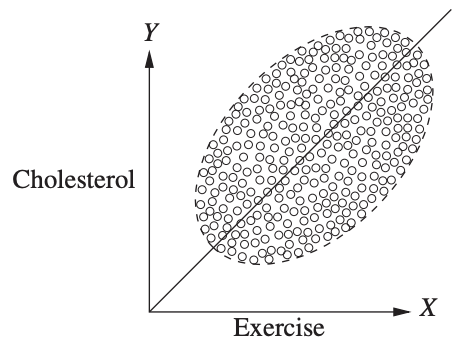
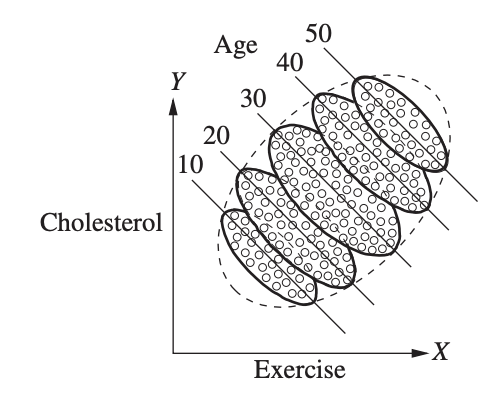
下一次根据统计结果给出结论时,无论结果和你的预期 [直觉|第六感|推理|经验] 多么一致,都记得多想一步哟。看看自己是否遗漏了可能的confounder呢?
Mediation Bias
Mediation Bias最常发生在控制了不该控制的变量而导致影响被人为削弱。在传统统计学中,因为没有引入因果推理,本着控制一切能控制的变量来做分析的原则,往往会在不经意间踩进Mediation的深坑。同时Mediation Analysis也是AB实验后续分析中有很高实用价值的一个方向,有机会咱在AB实验高端玩法系列中好好聊聊。
变量控制并非越多越好 - 案例3. 今天你又吃药了吗?
还记得上面心脏病药物实验么?当时我们给出的结论是应该分男女分别计算实验效果,因为性别是药物效果的Confounder。这里让我们把性别因素换成患者血压,并以此告诉大家分组计算并不是永远正确的。
数据和案例1一样,只不过这里的分组变量变成了患者血压。
这里加入新的假设,已知高血压是导致心脏病发作的原因之一,且该药物理论上有降血压的效果,因此医生想要检验该药物对防治心脏病的效果。
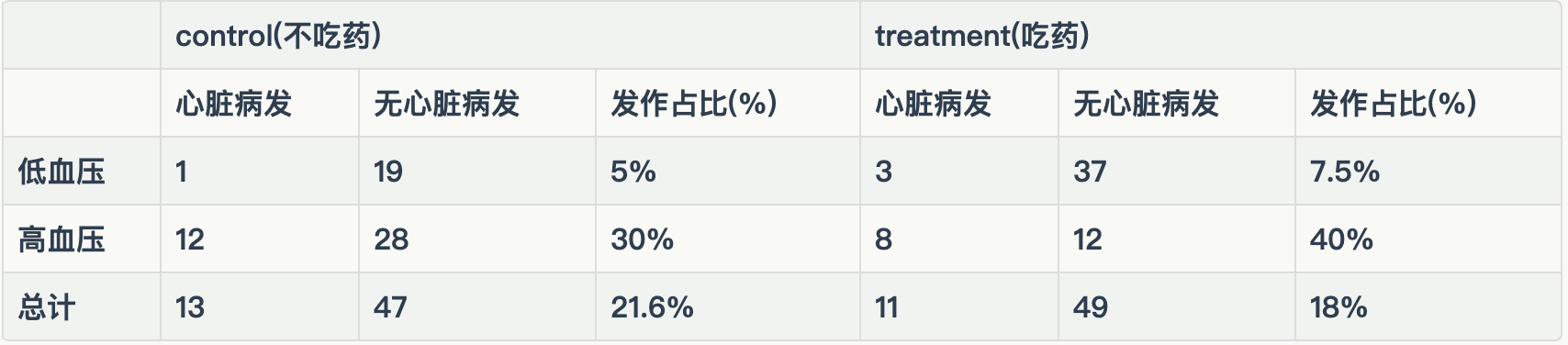
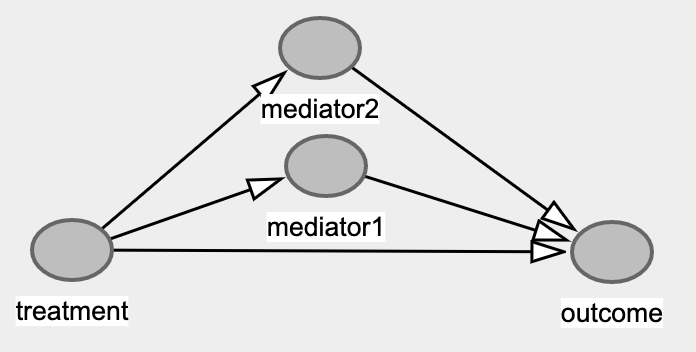
因为是观测性实验,如果从传统分析的角度,我们似乎应该控制一切能控制的变量,保证人群一致。但根据假设,结合数据我们能发现服药患者中高血压占比显著下降,这时降血压成为药物降低心脏病发作的一个Mediator,也就是部分药物效果通过降低血压来降低心脏病发概率。因果图如下

这种情况下如果我们按血压对患者分组,相当于Condition on Mediator,人为剔除了药物通过控制血压保护心脏的效果,会造成药物影响被人为低估。因此应该合并计算,药物对控制心脏病是有效的。
在分析观测数据时,并非一切变量都应该被控制。 一切处于treatment和outcome因果路径上的变量都不应该被控制。这里直接计算整体效果是合理的
Collidar Bias - BERKSON PARADOX
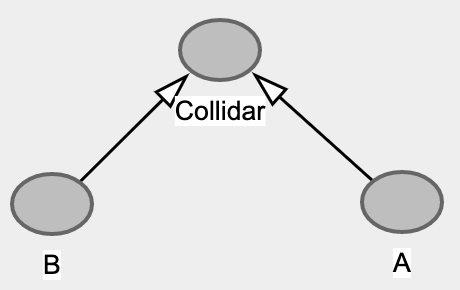
Collidar 最直观的影响是伪相关关系, 往往发生在对局部样本进行分析时,因为忽略了样本本身的特点从而得到一些非常奇葩的相关关系。
负‘相关’- 案例4. 孕妈妈应该吸烟?!
1959年的一项关于新生儿的研究中出现了有趣的数据:
- 已有研究表明孕妈妈吸烟会造成新生儿平均体重偏低
- 已有研究表明体重过轻(<5.5磅)的新生儿存活率显著偏低
- 该实验数据发现在体重过轻(<5.5磅)的新生儿中,妈妈吸烟的宝宝存活率显著高于妈妈不吸烟的宝宝
这是正正得负的节奏。。。>_<
还记得上面我们说Collidar Bias最容易在分析局部样本时发生,而这里体重过轻的新生儿明显就是局部样本。让我们画一个最简单的因果图答案就很明显了。
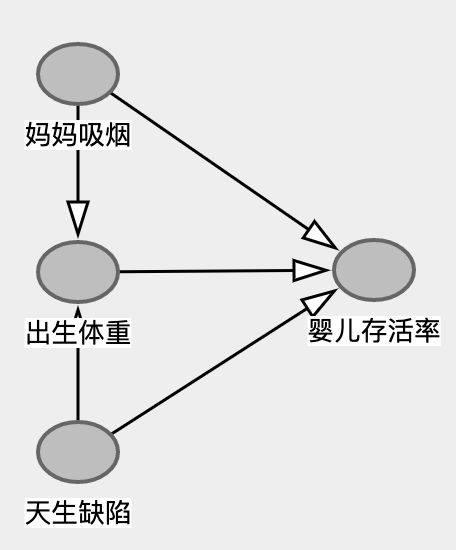
通过只观察体重过轻的新生儿存活率,我们一脚踩进了Collidar='出生体重过轻'这个陷阱,因为Condition on Collidar,从而让两个本来无关的原因出现了负向关系。简单讲,就是新生儿缺陷和妈妈吸烟都有可能导致新生儿体重过轻,两个因素此消彼长,当已知妈妈吸烟的时候,新生儿缺陷的概率会下降。而天生缺陷导致的体重过轻对婴儿存活率的影响更大是一个合理推断。因此孕妈妈吸烟反而会导致存活率上升。
上面的DAG并不完整,比如妈妈吸烟也有可能直接引起新生儿缺陷等等。但至少Collidar的存在在这里是很有说服力的
正‘相关’- 案例5. 呼吸道疾病和骨科疾病有关系?
因为Collidar而产生伪关联的变量往往是负相关的,就像上面的例子,也称explain-away effect。简单理解就是A,B都导致Collidar,那控制Collidar,A多了B就少了。但下面这个例子却是Collidar产生伪正向关系。
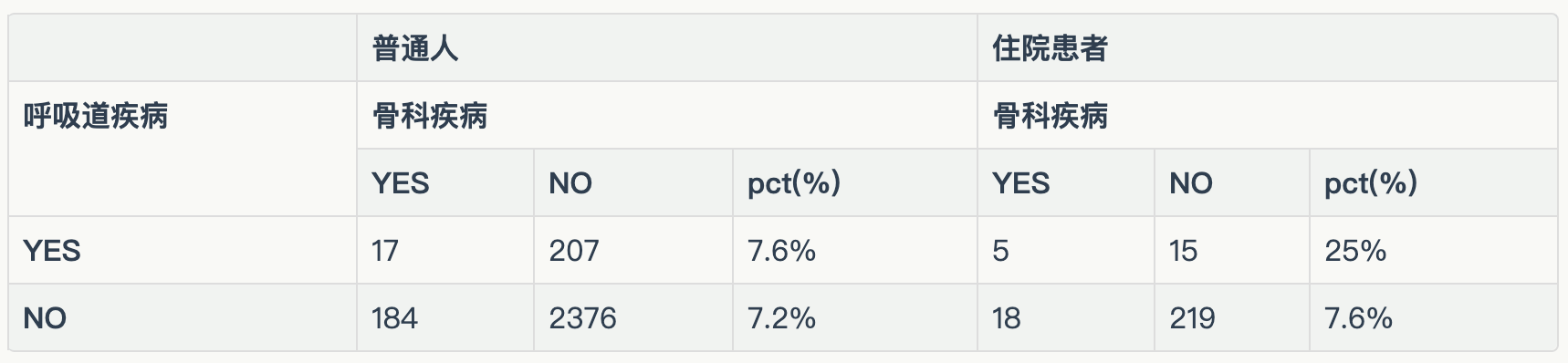
观察数据不难发现,对普通百姓而言患呼吸道疾病和骨科疾病没啥关系。但如果只看住院患者,患呼吸道疾病的患者同时患骨科疾病的概率会显著提升3倍以上!
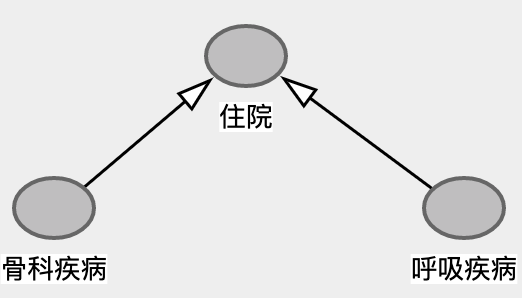
这个案例的DAG很好画,但是为什么这里不是负效应而是正效应呢?一种解释是单独呼吸疾病,或者骨科疾病直接导致住院的概率都很小,因此这里对于Collidar=‘住院’,两种疾病形成互补效应而非替代效应,既同时患有两种疾病的患者住院概率更高。因此只看住院患者就产生了伪正向关系。
上述DAG并不是唯一的可能,也有可能是患者的其他疾病导致住院的同时,导致患呼吸道和骨科疾病的概率上升。Anyway只看到以上数据是无法给出结论的,因此在分析局部样本的时候请格外小心
序章的案例就分享这么多,开始怀疑人生了有没有?!
Ref
- https://towardsdatascience.com/why-every-data-scientist-shall-read-the-book-of-why-by-judea-pearl-e2dad84b3f9d
- Judea Pearl, The Book of Why, the new science of casue and effect