推荐系统模型演化
LR-->GBDT+LR
FM-->FFM-->GBDT+FM|FFM
FTRL-->GBDT+FTRL
Wide&DeepModel (Deep learning era)
将从以下3方面进行模型分析:
1.why(模型设计背后的原理)
2.how(具体怎么设计,如何应用)
3.discussion(模型讨论)
Wide&Deep
- why
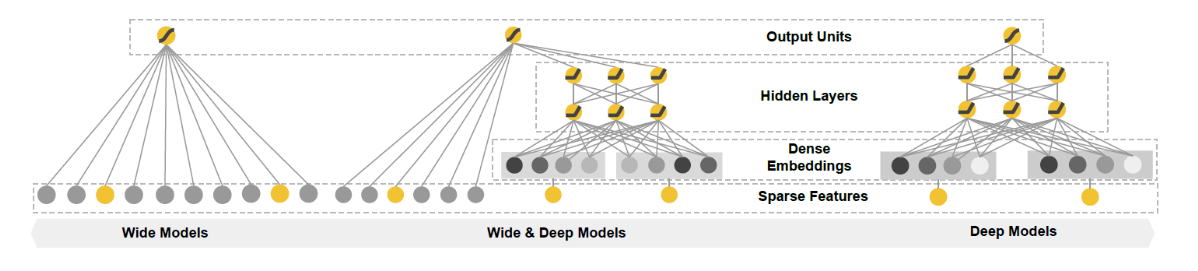
Memorization 和 Generalization
假如你设计了一个外卖推荐系统gugu,用户睡觉醒来需要点个外卖,推荐系统推荐给用户了一个烤肉饭,用户如果购买了就标记为1,否则为0(说明不是一个好的推荐)。点击率预估就是衡量推荐系统的一个线下指标。
wide(memorization)
那如何对用户合适的商品呢,我们需要记住用户的爱好。所以,你设计了几个相关的特征,用一个简单的线性模型学习这些特征的权重组合,模型会预测对特定产品的点击概率, gugu2.0上线了。一段时间后,用户吃腻了,需要换个口味,但是模型只记住了特定的模式。对一些训练集中未出现的组合特征,由于模型没有见过,记忆中没有关于这个特征的信息,导致模型单一,用户就会不满意。
deep(generalization)
为了推荐一些新的食物而且和用户之前点的食物相关,但是要口味不一样。模型需要能都捕捉到食物之间的内在联系,普通的离散特征无法满足这一要求,embedding引入了低维稠密向量表示离散特征的方法,相似的食物在embedding的一些维度上可能是一样的。比如口水鸡和椒麻鸡,经过embedding用4个维度[鸡肉,辣,麻,甜]表示
[0.52,0.23,0.312,0.002] [0.52,0.23,0.45,0.002]
使用embedding后的稠密向量,可以充分挖掘不同食物的相似性,可以做出新的合理的推荐,使用前馈神经网络进行学习,对于没有见过的特征,由于深度学习的泛化能力,模型也可以做出不错的预测。但是你发现模型会过度泛化,当用户的行为比较稀疏时,gugu会推荐一些相关性较小的食物。
wide+deep
为什么不同时进行memorization和generalization呢?Wide&Deep联合线性模型和深度模型,利用两个模型的优点进行联合训练。
- how
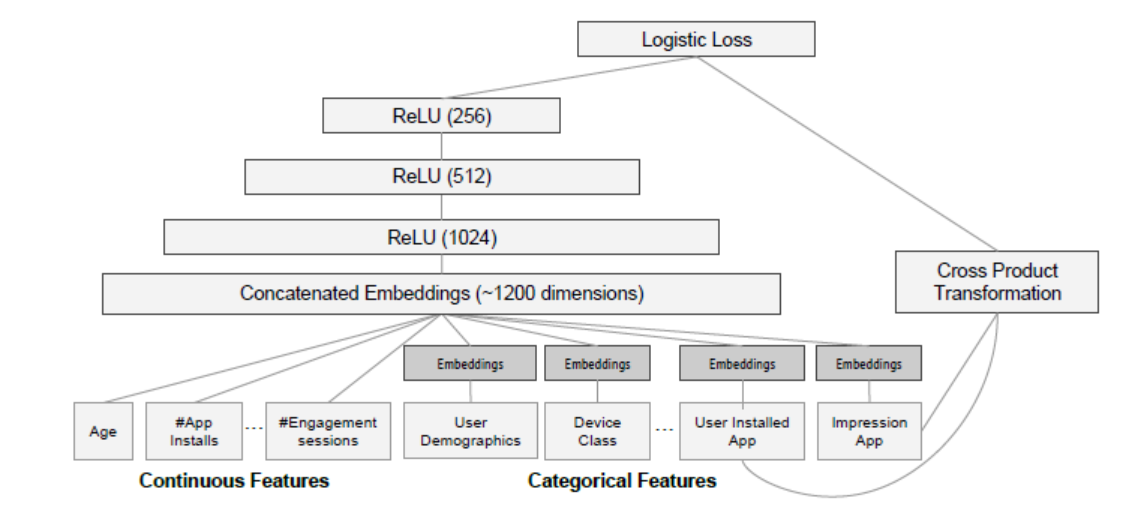
input
wide: 包括sparse类型的特征以及cross类型的特征等。原始输入特征和手动交叉特征
deep: 稠密特征,包括real value类型的特征以及embedding后特征
training
wide: (y=wx+b)
deep: (a^{(l+1)}=f(w^{(l)}a^{(l)}+b^{(l)}))
joint: (P(Y=1 | mathbf{x})=sigmaleft(mathbf{w}_{w i d e}^{T}[mathbf{x}, phi(mathbf{x})]+mathbf{w}_{d e e p}^{T} a_{f}^{left(l_{f} ight)}+b ight))
Wide部分用FTRL+L1来训练;Deep部分用AdaGrad来训练。 使用BP算法采用joint train的方式训练。
- discussion
1.利用wide和deep组合,wide手动交叉特征,deep对离散进行embedding
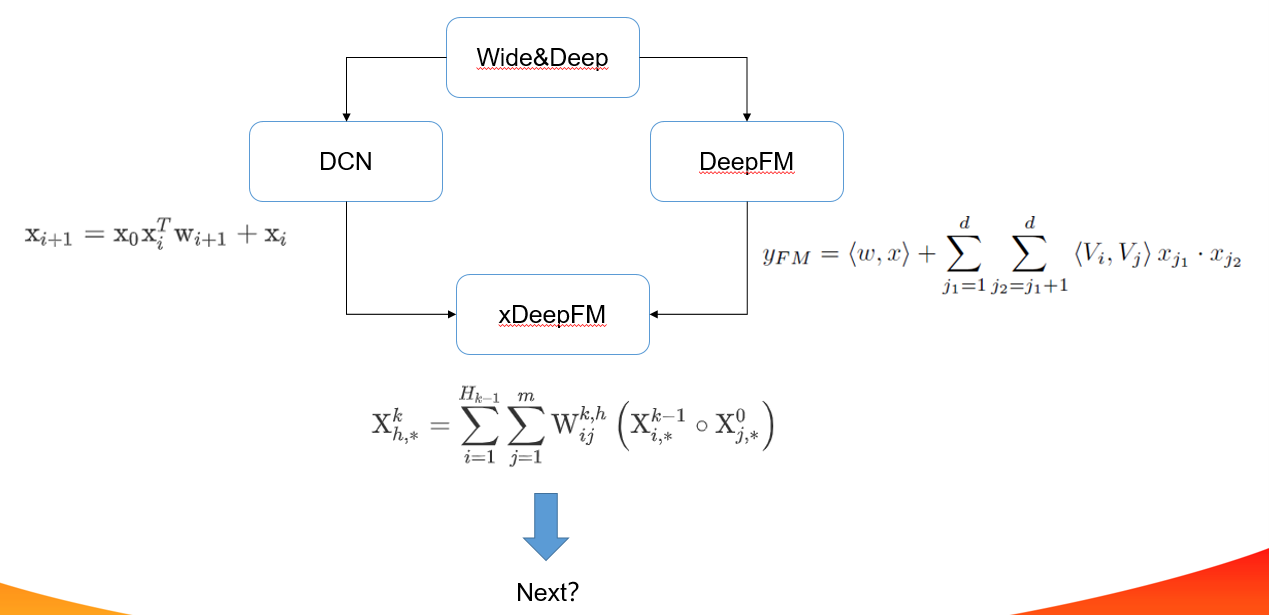
2.对wide部分进行改进,自动化交叉特征,DeepFM,DCN
3.embedding在线训练得到,可否离线预训练
4.deep部分进行改进,AFM
离散值低阶vector-wise交互;连续值高阶bit-wise交互
vector-wise和bit-wise文末有解释
DeepFM
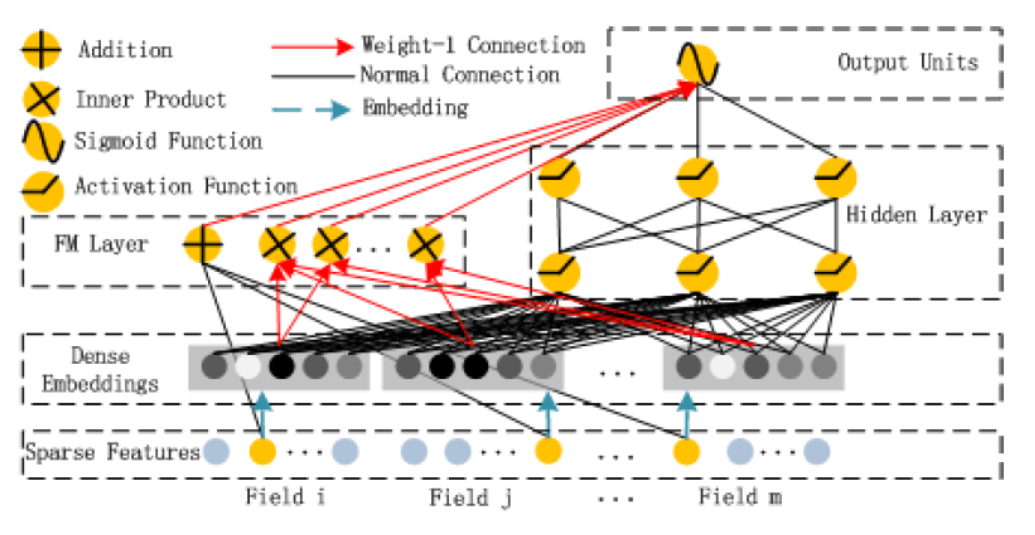
连续值离散化,低阶vector-wise组合,高阶bit-wise组合
DCN
- why
FM可以自动组合特征,但也仅限于二阶叉乘。告别人工组合特征,并且自动学习高阶的特征组合呢
(x1x2x3)
- how
拟合残差
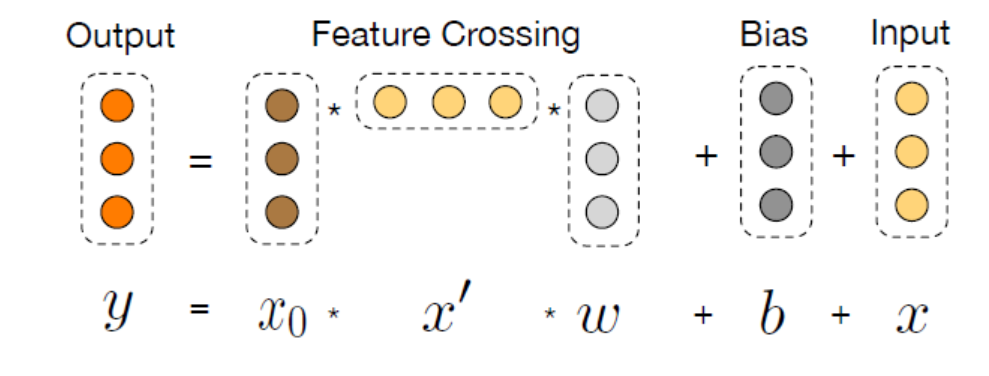
为什么work?

- discussion
-
显示的高阶特征组合,特征组合阶数随着网络深度增加而增加
-
复杂度线性增长,相比DNN更快
-
利用最后的高阶组合特征,实际高层特征组合已经包含了低层的组合,考虑单层的组合引入最后的计算
-
特征交互还是bit-wise,对模型记忆能力提升是否有帮助
-
是否真的学到了高阶特征交互?输出是输入的标量乘积
连续值离散化,高阶bit-wise组合
xDeepFm
- why
传统特征工程缺点:
1.好的特征需要专家知识
2.大数据量下无法无法手动交叉特征
3.手动交叉特征的无法泛化
FM对所有特征组合,引入噪声;FNN、PNN聚焦于高阶特征,忽略了低阶特征;
DNN学习高阶特征交互,但是学习到特征交互是隐含的,bit-wise级的,那么DNN是否真的有效在高阶特征处理上?CIN被设计在vector-wise级进行学习高阶特征
embedding: 不同样本的长度不同,但embedding维度是一样的
隐式高阶特征:bit-wise
显示高阶特征交互: DCN,输出受限于和x0的交互、bit-wise
CIN(Compressed Interaction Network(CIN))
DCN没有有效的学习到高阶特征交互,输出是x0的标量乘积
但是标量并不意味着线性!!!
- how
bit-wise到vector-wise
显示交互
复杂度非指数级增长
取前一层的(H_{k-1})的个vector,与输入层的
个vector,进行两两Hadamard乘积运算,得到(H_{k-1}*m)个 vector,然后加权求和
第
层的不同vector区别在于,对这(H_{k-1}*m)个 vector 求和的权重矩阵不同。 (H_k)即对应有多少个不同的权重矩阵(W^k)
1.为什么做Hadamard积
保持维度不变,做到vector-wise级交互
2.vector-wise交互
网络的每一层计算是以embedding向量的方式进行哈达玛积,保持embedding的结构
3.每一层的输出由当前输入和隐状态共同决定,类RNN
4.类CNN(装饰)
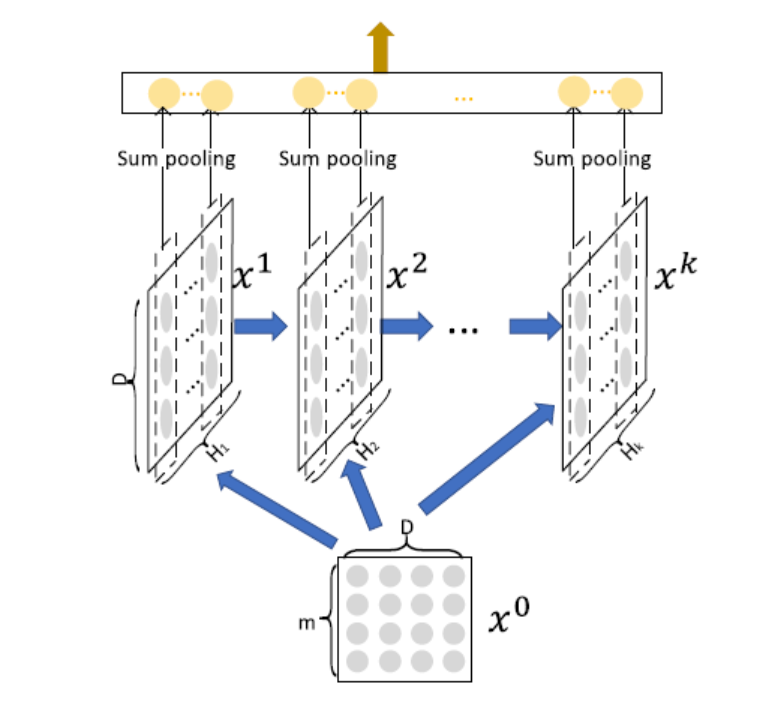
sum pooling 有效性:(p_{i}^{k}=sum_{j=1}^{D} mathrm{X}_{i, j}^{k})
当只有一层,sum pooling就是两两向量的内积之和,降为FM
组合
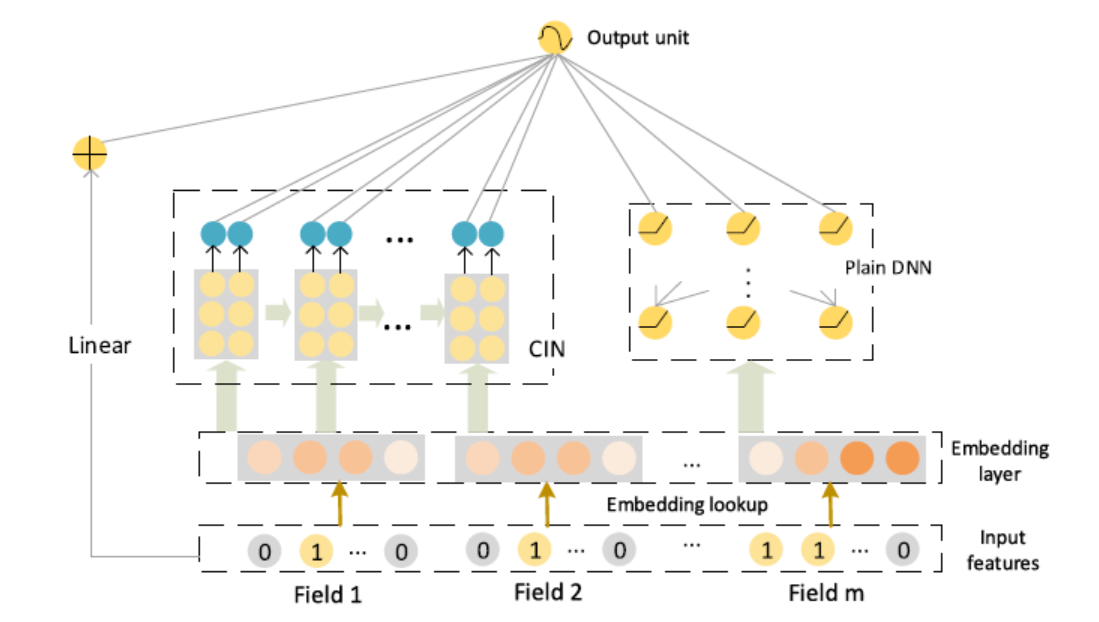
线性单元、DNN、CIN;记忆、泛化、记忆+泛化
1.CIN如何显示的执行特征交互
2.必须组合显示和隐式表达吗
3.xDeepFm参数设置影响
- discussion
1.特征交叉利用稠密向量进行,是否存在一个网络进行离散高阶向量级特征交互
2.交互深度改进,残差,全局信息观
连续值离散化,高阶bit-wise组合,CIN高阶vector-wise组合
bit-wise VS vector-wise
假设隐向量的维度为3维,如果两个特征(对应的向量分别为(a1,b1,c1)和(a2,b2,c2)的话)在进行交互时,交互的形式类似于f(w1 * a1 * a2,w2 * b1 * b2 ,w3 * c1 * c2)的话,此时我们认为特征交互是发生在元素级(bit-wise)上。如果特征交互形式类似于 f(w * (a1 * a2 ,b1 * b2,c1 * c2))的话,那么我们认为特征交互是发生在特征向量级(vector-wise)。
(x1=(a1,b1,c1),x2=(a2,b2,c2))
bitwise: (f(w1*a1*a2,w2*a2*b2,w3*a3*b3))
vector-wise: (f(w(a1*a2,a2*b2,a3*b3)))
explicitly VS implicitly
显式的特征交互和隐式的特征交互。以两个特征为例xi和xj,在经过一系列变换后,我们可以表示成 wij * (xi * xj)的形式,就可以认为是显式特征交互,否则的话,是隐式的特征交互。
reference:
https://zhuanlan.zhihu.com/p/55234968
Cheng H T, Koc L, Harmsen J, et al. Wide & deep learning for recommender systems[C]//Proceedings of the 1st workshop on deep learning for recommender systems. ACM, 2016: 7-10.
Guo H, Tang R, Ye Y, et al. DeepFM: a factorization-machine based neural network for CTR prediction[J]. arXiv preprint arXiv:1703.04247, 2017.
Wang R, Fu B, Fu G, et al. Deep & cross network for ad click predictions[C]//Proceedings of the ADKDD'17. ACM, 2017: 12.
Lian J, Zhou X, Zhang F, et al. xdeepfm: Combining explicit and implicit feature interactions for recommender systems[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM, 2018: 1754-1763.