树状数组
一、原理分析及操作模板
1、用处:
-
快速求前缀和
O(log n) -
修改某一个数
O(log n)与前缀和、差分的对比:
-
前缀和:在
O(1)下求前缀和,在O(n)下修改某个数 -
差 分:在
O(n)下求前缀和,在O(1)下修改某个数综合考虑复杂度在
O(n)
2、原理分析:
基于二进制: $ x = 2^{i_k} + 2^{i_{k-1}} + ... + 2^{i_1}$ 其中 $ i_k geq i_{k-1} geq i_{k-2} geq ... geq i_1, k leq log_2 x $
将其划分为k个区间:
- ((x-2^{i_1}, x]) 区间长度:(2^{i_1})个数, (2^{i_1})是x二进制表示的最后一位1。
- ((x-2^{i_1}-2^{i_2}, x-2^{i_1}]) 区间长度:(2^{i_2})个数, (2^{i_2})是(x-2^{i_1})二进制表示的最后一位1。
- ......
... ((0,x-2^{i_1}-2^{i_2}-...-2^{i_{k-1}}]) 区间长度:(2^{i_k})个数, (2^{i_k})是(x-2^{i_1}-2^{i_2}-...-2^{i_{k-1}})二进制表示的最后一位1。
=> (L, R] 长度一定是R二进制表示的最后一位1所对应的次幂
=>[R - lowbit(R) + 1, R]
=>设tr[N]是树状数组,则 tr[x] = sum [x - lowbit(x) + 1, x]
=>如此,就可以在O(log n)下求出1~x的和
原理图:
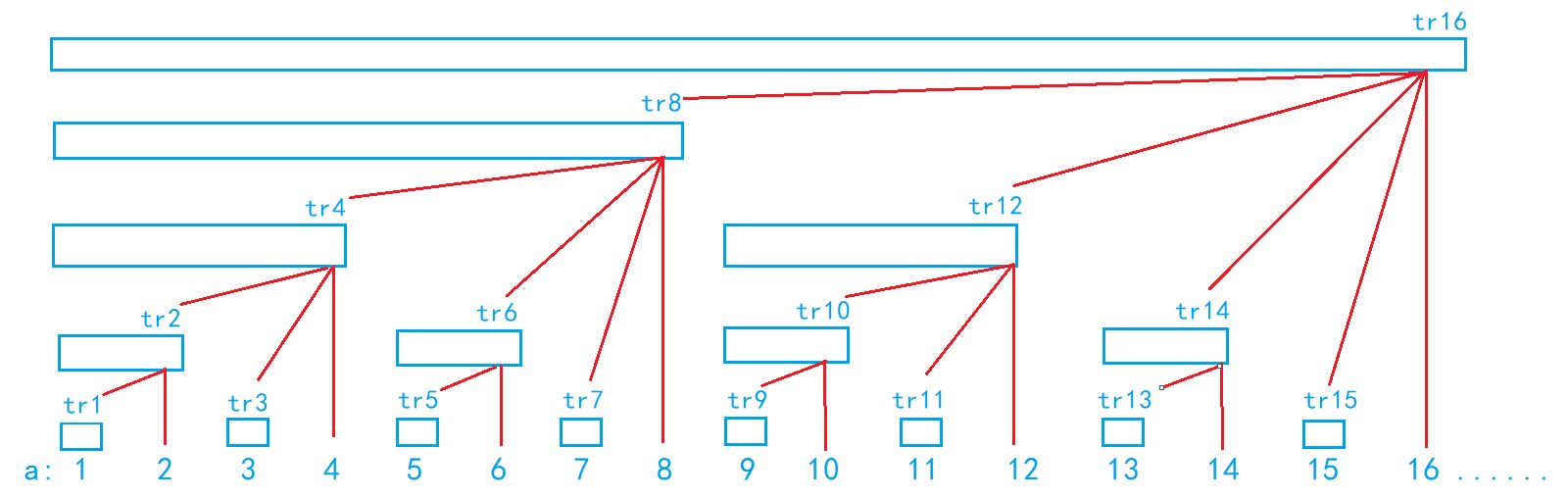
1)通过父节点找子节点(理解过程,实际不会用到)
[x = ......1underbrace{00...00}_{k个}\
tr[x] = 以x结尾的,长度是2^k的区间和\
= x + [x - 2^k + 1, x - 1]\
\
x-1 = ......0underbrace{11...11}_{k个}
ightarrow 每一个1对应了1个子节点\
left{
egin{aligned}
(...01...10, ...01...11]\
(...01..100, ...01...10]\
......\
(...00...00, ...010...0]
end{aligned}
ight.\
推得:tr[x] = x + tr[x-1] + tr[x -1 - lowbit(x-1)] + ... + tr[i]quad i>0
]
2)通过子节点找父节点(对应修改操作)
当前值节点:$ x = ...0underbrace{1...10...0}_{k位}$
直接父节点:(p=...1underbrace{0......0}_{k位}) (Rightarrow) p = x + lowbit(x) //最多持续logx次
3、代码模板
//lowbit操作
int lowbit(int x)
{
return x & -x;
}
//添加(修改)操作
void add(int x, int c)
{
for(int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
//查询操作,求x的前缀和
int sum(int x)
{
int res = 0;
for(int i = x; i; i -= lowbit(i)) ans += tr[i];
return ans;
}
4、扩展
tr[]维护前缀和:单点加,区间求和tr[]维护差分:区间加,单点求和
二、相关题目
241.楼兰图腾
242.一个简单的整数问题
用树状数组维护差分数组,实现区间加,单点求和
243.一个简单的整数问题2
用树状数组维护差分数组,实现区间加,区间求和
244.谜一样的牛
树状数组+二分