PaperRead

Moller T. A fast triangle-triangle intersection test[J]. Journal of Graphics Tools, 1997, 2(2): 25-30.

https://cn.bing.com/academic/profile?id=8f3b04bb774f7be38107ff2d63d056b5&encoded=0&v=paper_preview&mkt=zh-cn#

来描述下已知条件：

• 三角形(T_1)和(T_2);
• 三角形(T_1)的顶点为(V_0^1,V_1^1,V_2^1),三角形(T_2)的顶点为(V_0^2,V_1^2,V_2^2);
• 三角形(T_1)所在的平面为(pi_1);三角形(T_2)所在的平面为(pi_2)。

首先确定平面(pi_2)的方程如下：

[N_2cdot X + d_2 = 0 ]

其中X是平面上的任意一点，(N_2)和(d_2)如下：

[N_2 = (V_1^2 - V_0^2) imes (V_2^2 - V_0^2) \ d_2 = -N_2 cdot V_0^2 ]

上面公式就是平面方程的一般形式，可以写成如下形式，更加容易理解：

[N_2cdot (X - V_0^2) = 0 ]

那么三角形(T_1)的三个顶点到平面(pi_2)的距离可以通过带入上面的公式直接计算得到，如下：

[d_{V_i^1} = N_2 cdot (V_i^1 - V_0^2), i=0,1,2 ]

如果(d_{V_i^1} e 0)，并且所有的值都有相同的符号，那么三角形(T_1)位于平面(pi_2)的一侧，那么三角形之间是没有交叠的；对于三角形(T_2)和平面(pi_1)也用相同的处理方式。

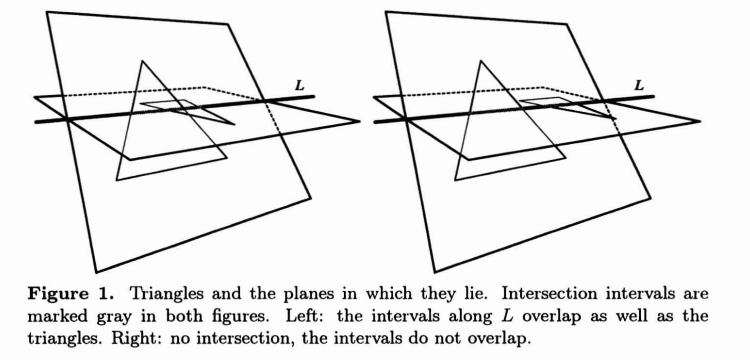
如果所有的(d_{V_i^1} = 0)，那么三角形是共面的；如果不是，那么平面(pi_1)和(pi_2)相交一条线，(L = O + tD)，其中(D = N_1 imes N_2)是线的方向，(O)是线上的一个点。如果相交的线段有重叠，那么两个三角形相交，如下图。

直线L与三角形，相交段计算。假设我们需要计算三角形(T_1)和直线(L)之间的相交线段，假设(V_0^1)和(V_2^1)位于平面(pi_2)的同一侧，(V_1^1)位于平面的另一侧。先将顶点投影到直线L上，如下：

[p_{V_i^1} = Dcdot (V_i^1 - O) ]

从上图可见，三角形(V_0^1BK_0^1)和三角形(V_1^1BK_1^1)相似。那么可以得到：

[t_1 = p_{V_0^1} + (p_{V_1^1} - p_{V_0^1})frac{d_{V_0^1}}{d_{V_0^1} - d_{V_1^1}} ]

同理可得t2，同理可以得到三角形(T_2)上的相交线段。

如果两个线段有重叠，那么两个三角形相交。

如果两个三角形共面。那么将三角形投影到能够得到最大面积的axis-aligned plane上。接下来执行二维三角形相交测试即可。

优化

由于L线上的重叠关系是针对线段区间的，只针对相交测试的话，求(p_{V_i^1})的公式可以简化为：

[p_{V_i^1} = Dcdot V_i^1, i=0,1,2 ]

又由于重叠关系在投影到最近的一条轴上的时候，仍然保留，因此可以进一步简化为：

[p_{V_i^1} = left{ egin{array}{rcl} V_{ix}^1, if |D_x| = max(|D_x|, |D_y|, |D_z|) \ V_{iy}^1, if |D_y| = max(|D_x|, |D_y|, |D_z|) \ V_{iz}^1, if |D_z| = max(|D_x|, |D_y|, |D_z|) \ end{array} , i=0,1,2. ight. ]

小结

整个算法流程如下：

1. 计算三角形2的平面方程；
2. 如果三角形1的顶点都在三角形2的同一侧，那么不相交；
3. 计算三角形1的平面方程；
4. 如果三角形2的顶点都在三角形1的同一侧，那么不相交；
5. 计算两个平面的相交线，并投影到最大的轴上；
6. 计算相交线和每个三角形的相交的线段；
7. 判断两个三角形的上相交的线段之间的关系；

目前算法对于三角形退化成直线或点的情况没有考虑。

Others

其他类似的判断三角形相交的算法见：快速检测空间三角形相交算法的代码实现(Devillers & Guigue算法)