欧拉回路和欧拉通路

据说流经哥尼斯堡的普雷格尔河中有两个岛，两个岛与两岸共4处陆地通过7座杨 彼此相联，当地居民们热衷于一个难题：是否存在一条路线，可以不重复地走遍7座桥，这就是著名的七桥问题。

它由欧拉首先提出并给出了完美的解答。

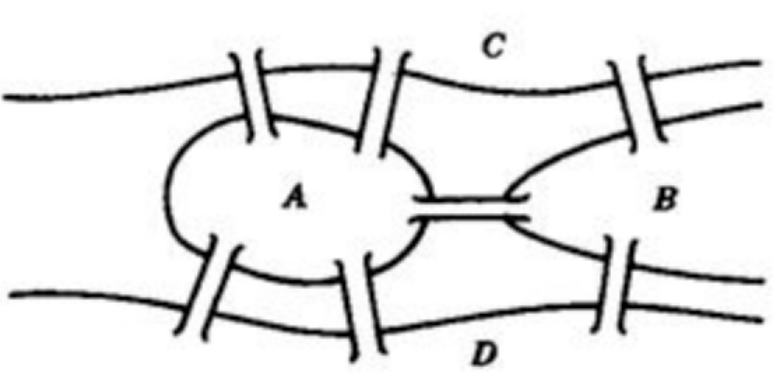
用图论的语言转换为

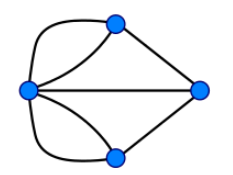
不难发现，欧拉道路中，出和入是对应的——除了起点和终点外，其他点的进出次数应该相同（即除终点和起点外，其他点的度应该是偶数）但是在七桥问题中，四个点的度都是奇数，这样的点被称为奇点，

因此七桥问题不存在欧拉道路。上述条件也是充分条件——如果一个无向图是连通的，且最多只有两个奇点，则必须从其中一个奇点出发，另一个奇点终止；如果奇点不存在，则可以从任意点出发，最终一定会回到终点。

由此也能推出有向图的结论：最多只能有两个点的入度不等于出度，而且必须是其中一个点的出度恰好比入度大1（把它作为起点），另一个的入度比出度大一（作为终点），或者每个点入度等于出度，还有一个前提条件：在忽略边的方向后，图必须是连通的。

欧拉通路与欧拉回路意义并不相同，欧拉回路要能够回到起点

 无向图是否具有欧拉通路或回路的判定:

欧拉通路:图连通；图中只有0个或2个度为奇数的节点

欧拉回路:图连通；图中所有节点度均为偶数

 有向图是否具有欧拉通路或回路的判定:

欧拉通路:图连通；除2个端点外其余节点入度=出度；1个端点入度比出度大1；一个端点入度比出度小1 或 所有节点入度等于出度

欧拉回路:图连通；所有节点入度等于出度

那做道题应用下学到的新知识吧

HDU 1878 欧拉回路（并查集+欧拉回路）

#include <algorithm>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <iostream>
#include <cstdlib>
#include <set>
#include <vector>
#include <cctype>
#include <iomanip>
#include <sstream>
#include <climits>
#include <queue>
#include <stack>
using namespace std;
typedef long long ll;
#define INF 0X3f3f3f3f
const ll MAXN = 1e3 + 7;
const ll MOD = 1e9 + 7;
int pre[MAXN]; 
int n, m;
int degree[MAXN];
int find(int x) //查找根结点
{
    int r = x;
    while (r != pre[r]) //寻找根结点
        r = pre[r];
    int i = x, j;
    while (pre[i] != r) //路径压缩
    {
        j = pre[i];
        pre[i] = r;
        i = j;
    }
    return r;
}
int main()
{
    ios::sync_with_stdio(false);
    while (cin >> n && n)
    {
        cin >> m;
        memset(degree, 0, sizeof(degree));
        for (int i = 1; i <= n; i++)
            pre[i] = i;
        while (m--)
        {
            int a, b;
            cin >> a >> b;
            int fa = find(a);
            int fb = find(b);
            if (fa != fb)
            {
                pre[a] = b;
                degree[a]++;
                degree[b]++;
            }
        }
        int flag = 1;
        for (int i = 2; i <= n; i++)
        {
            if (degree[i] & 1 || pre[i] != pre[1])
            {
                flag = 0;
                break;
            }
        }
        cout << flag << endl;
    }
    return 0;
}