【CF EDU59 D】Compression

题意

给定一个n阶方阵A,现在要从里面取出一个n/x阶子方阵B，使得使得对于对于A中每一个元素，都有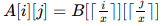
,求x的最大值

分析

考虑这个关系式

(frac{i}{x}-1 = frac{i-x}{x})

也就是说，(B[frac{i}{x}][frac{j}{x}] = A[i-x+p][j-x+q] (1leq p,q leq x))

可以看出这是一个x阶子方阵矩阵

其实我们要求的就是将A平均分割成(frac{n}{x}×frac{n}{x})个x阶方阵，每个方阵内的元素全都相等，求最大的x

我在这里维护了一个二维前缀和，这样对于一个子矩阵，只有和为0，或者和为矩阵的大小的时候满足元素全都相等的条件

根号n暴力枚举X即可求得答案

代码

#include<bits/stdc++.h>
using namespace std;
int a[5201][5201];
int n;
int input(){
    char ch;
    scanf(" %c",&ch);
    if(ch<='9'&&ch>='0') return ch-'0';
    return ch-'A'+10;
}
int main() {
    scanf("%d",&n);
    for(int i=1;i<=n;i++) {
	for(int j=1;j<=n;j+=4) {
	    int now = input();
	    for(int k=j,o=3;o>=0;k++,o--){
		a[i][k] = a[i-1][k] + a[i][k-1] - a[i-1][k-1] + ((now>>o)&1);
	    }

	}
    }
    int maxx = 0;
    for(int i=1;i*i<=n;i++) {
	if(n%i)continue;
	int _ = i;
	bool flag = 0;
	for(int xbe = 1,xen = _;xbe<=n;xbe+=_,xen+=_) {
	    for(int ybe = 1,yen = _;ybe<=n;ybe+=_,yen+=_){
		int sum = a[xen][yen]- a[xbe-1][yen] - a[xen][ybe-1] + a[xbe-1][ybe-1];
		if(sum !=0 && sum != _*_) {
		    flag = 1;
		    break;
		}
	    }
	    if(flag)break;
	}
	if(flag == 0) maxx = max(maxx,_);
	if(n/i!=_){
		_ = n/i;
	    bool flag = 0;
	    for(int xbe = 1,xen = _;xbe<=n;xbe+=_,xen+=_) {
		for(int ybe = 1,yen = _;ybe<=n;ybe+=_,yen+=_){
		    int sum = a[xen][yen]- a[xbe-1][yen] - a[xen][ybe-1] + a[xbe-1][ybe-1];
		    if(sum !=0 && sum != _*_) {
			flag = 1;
			break;
		    }
		}
		if(flag)break;
	    }
	    if(flag == 0) maxx = max(maxx,_);

	}
    }
    cout<<maxx<<endl;
}