拓扑排序入门（真的很简单）

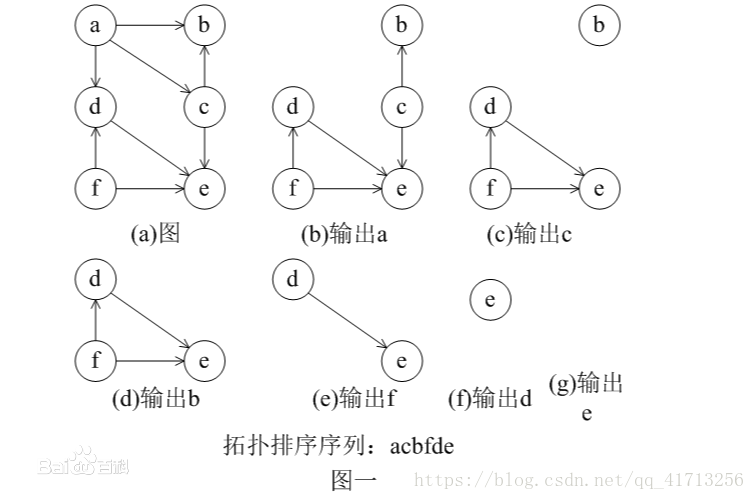
在一个有向图中，对所有的节点进行排序，要求没有一个节点指向它前面的节点。
先统计所有节点的入度，对于入度为0的节点就可以分离出来，然后把这个节点指向的节点的入度减一。
一直做改操作，直到所有的节点都被分离出来。
如果最后不存在入度为0的节点，那就说明有环，不存在拓扑排序，也就是很多题目的无解的情况。

下面是算法的演示过程。

下面是我以前的写法，比较好理解，但是效率低

//b[]为每个点的入度
for(i=1;i<=n;i++){
for(j=1;j<=n;j++){
if(b[j]==0){ //找到一个入度为0的点
ans=j;
vis[cnt++]=j;
b[j]--;
break;
}
}
for(j=1;j<=n;j++)
if(a[ans][j]) b[j]--; //与入度为0的点相连的点的入度减一
}
printf("%d",vis[0]);
for(i=1;i<cnt;i++) printf(" %d",vis[i]);
printf("\n");

下面是我现在一直以来的写法，O(V+E)。点数+边书

queue<int>q;
vector<int>edge[n];
for(int i=0;i<n;i++) //n 节点的总数
if(in[i]==0) q.push(i); //将入度为0的点入队列
vector<int>ans; //ans 为拓扑序列
while(!q.empty())
{
int p=q.front(); q.pop(); // 选一个入度为0的点，出队列
ans.push_back(p);
for(int i=0;i<edge[p].size();i++)

{

int y=edge[p][i];

in[y]--;

if(in[y]==0)

q.push(y);

}

}

if(ans.size()==n)

{

for(int i=0;i<ans.size();i++)

printf( "%d ",ans[i] );

printf("\n");

}

else printf("No Answer!\n"); // ans 中的长度与n不相等，就说明无拓扑序列

有些拓扑排序要求字典序最小什么的，那就把队列换成优先队列就好了。

例如：ZCMU-2153点击打开链接

代码：

1. #include<bits/stdc++.h>

2. using namespace std;

3. typedef long long LL;

4. const int inf=1e9;

5. const int maxn=1e6+5;

6. vector<int>edge[50];

7. int in[50];

8. int main()

9. {

10. char s[5];

11. set<int>k;

12. while(cin>>s)

13. {

14. k.insert(s[2]-'A');

15. k.insert(s[0]-'A');

16. if(s[1]=='>')

17. {

18. in[s[2]-'A']++;

19. edge[s[0]-'A'].push_back(s[2]-'A');

20. }

21. else

22. {

23. in[s[0]-'A']++;

24. edge[s[2]-'A'].push_back(s[0]-'A');

25. }

26. }

27. priority_queue<int,vector<int>,greater<int> >q;

28. for(int i=0;i<30;i++)

29. {

30. if(in[i]==0&&k.count(i)!=0)

31. q.push(i);

32. }

33. vector<int>ans;

34. while(!q.empty())

35. {

36. int p=q.top(); q.pop();

37. ans.push_back(p);

38. for(int i=0;i<edge[p].size();i++)

39. {

40. int y=edge[p][i];

41. in[y]--;

42. if(in[y]==0&&k.count(y)!=0)

43. q.push(y);

44. }

45. }

46. if(ans.size()==k.size())

47. {

48. for(int i=0;i<ans.size();i++)

49. printf("%c",ans[i]+'A');

50. printf("\n");

51. }

52. else printf("No Answer!\n");

53. return 0;

54. }

还有一种比较坑的排序 要求编号小的尽量排在前面，这里与字典序最小是不一样的，看一下例题。

HDU-4857 点击打开链接

逃生

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 6725    Accepted Submission(s): 1965

Problem Description

糟糕的事情发生啦，现在大家都忙着逃命。但是逃命的通道很窄，大家只能排成一行。

现在有n个人，从1标号到n。同时有一些奇怪的约束条件，每个都形如：a必须在b之前。
同时，社会是不平等的，这些人有的穷有的富。1号最富，2号第二富，以此类推。有钱人就贿赂负责人，所以他们有一些好处。

负责人现在可以安排大家排队的顺序，由于收了好处，所以他要让1号尽量靠前，如果此时还有多种情况，就再让2号尽量靠前，如果还有多种情况，就让3号尽量靠前，以此类推。

那么你就要安排大家的顺序。我们保证一定有解。

Input

第一行一个整数T(1 <= T <= 5),表示测试数据的个数。
然后对于每个测试数据，第一行有两个整数n(1 <= n <= 30000)和m(1 <= m <= 100000)，分别表示人数和约束的个数。

然后m行，每行两个整数a和b，表示有一个约束a号必须在b号之前。a和b必然不同。

Output

对每个测试数据，输出一行排队的顺序，用空格隔开。

Sample Input

15 103 51 42 51 23 41 42 31 53 51 2

Sample Output

1 2 3 4 5

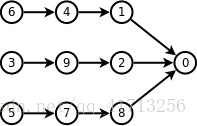
举个例子如图：

如果你用优先队列拓扑排序得到的是：3 5 6 4 1 7 8 9 2 0

但是正确答案为 6 4 1 3 9 2 5 7 8 0 这样使得小的（1）尽量在前面。

这里我们可以得到 前面的小的不一定排在前面，但是有一点后面大的一定排在后面。

我们看 6和3不一定3排在前面，因为6后面连了一个更小的数字1能使得6更往前排。

在看 2和 8，8一定排在后面，因为8后面已经没有东西能使它更往前排（除了0）。

所以最后我们的做法就是 建立一个反图，跑一边字典序最大的拓扑排序，最后再把这个排序倒过来就是答案了。

1. #include<iostream>

2. #include<cstdio>

3. #include<cstring>

4. #include<algorithm>

5. #include<vector>

6. #include<queue>

7. using namespace std;

8. typedef long long ll;

9. vector<int>edge[30010],ans;

10. priority_queue<int>q;

11. int in[30010];

12. int T,n,m;

13. void init()

14. {

15. for(int i=1;i<=n;i++)

16. {

17. edge[i].clear();

18. in[i]=0;

19. }

20. while(!q.empty()) q.pop();

21. ans.clear();

22. }

23. void solve()

24. {

25. int i,j;

26. for(i=1;i<=n;i++)

27. if(in[i]==0) q.push(i);

28. while(!q.empty())

29. {

30. int p=q.top(); q.pop();

31. ans.push_back(p);

32. for( i=0; i<edge[p].size(); i++ )

33. {

34. int v=edge[p][i];

35. in[v]--;

36. if(in[v]==0) q.push(v);

37. }

38. }

39. for(i=ans.size()-1;i>0;i--)

40. printf("%d ",ans[i]);

41. printf("%d\n",ans[0]);

42. }

43. int main()

44. {

45. int a,b;

46. scanf("%d",&T);

47. while(T--)

48. {

49. scanf("%d%d",&n,&m);

50. init();

51. while(m--)

52. {

53. scanf("%d%d",&a,&b);

54. edge[b].push_back(a);

55. in[a]++;

56. }

57. solve();

58. }

59. return 0;

60. }