warning:
如果想优雅快速的切掉此题以及不屑于写平衡树的可以走了QVQ。
简化の题目:
一个仅可沿平行于坐标轴方向移动的平面直角坐标系,在方阵中有 (P(1≤P≤10^5))个跳板,第i个跳板位于((x1_i,y1_i)),当移至第i个跳板时,将会去到((x2_i,y2_i)(x2_i ge x1_i,y2_i ge y1_i))(不计为移动)。已知每个跳板的起点,终点均无重点,求由 ((0,0)) 移至 ((n,n)) 最少的移动距离。
约定
- 所有的 (k) 表示的都是某个 (y) 坐标
- (K)表示查询的(y)坐标
思路
由于之前做过看起来类似的题,所以我很快想到了扫描线。
把每个端点从 (0)~(k) 转移过来即可
但是,扫描线要用线段树维护,非常明显的线段树会被卡掉。
此时:
别人:离散化
本蒟蒻:平衡树
没错,我们要用以排名排序的平衡树来维护区间!
于是我愉快的抄起我从没拿来写过题的Treap头铁平衡树。
实际模板上几乎都没写过,还边写边想FHQ Treap更好写-
然后打了2h拿了26.7分TAT
做法
emm,其实会平衡树的话几乎不用想,这里说下几个坑点好了。
-
墙裂建议使用FHQ-Treap写本题,思路清晰,代码优质,快速切题的不二之选。
讲完了,完结撒花
*★,°*:.☆( ̄▽ ̄)/$:*.°★*
emm,上面漏了一点:
,就是不会。
假如你像我一样不会FHQ-Treap ,只会一些转来转去转晕人的垃圾玩意 的话,那么:
-
维护(l),(r),(f)
(左右父),平衡性质要用的东西(没错就是Treap),当前点的坐标(k)(提前排序,这样就只剩一个坐标了),(V)(点的权值),(MaxY)(为其右节点的(MaxY),没有则为(k)),(Min)(为当前点的所有后代节点到(MaxY)的最小价值,维护起来相当坑爹) -
(Min)的转移:emm,上
奇丑无比的图吧!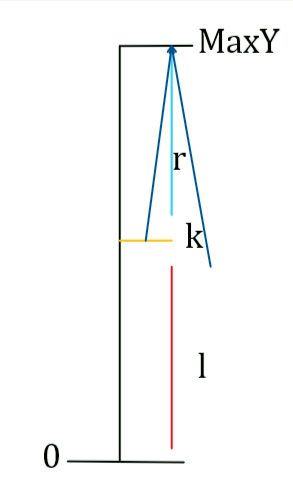
PS:所有的点维护的都是(0)~(Maxy)的区间,因为即使记录了左端点也用不上,因为所有询问询问的都是(0)~(k)的区间(emm,这句话没有语病)
(Maxy) 的转移明显
由图可得(其右节点的(MaxY),没有则为(k)),维护了(Maxy)之后就可以维护(Min)了,为:(min{)
( ext{左儿子的}Min+ ext{当前}Maxy- ext{左儿子的}Maxy,)
( ext{右儿子的}Min,)
(V+Maxy-k)
(})
我实在想不出怎么能更好看了-
(V)的值:emm,不好解释,反正就是查询K(- ext{跳板两端点的}x ext{坐标差}) 至于为什么自行意会……大概就是(y)坐标距离(-x)坐标上节省的距离。
幸好是静态的 -
查询:大坑点!大坑点!!大坑点!!!
- 如果查询包含这个区间,返回(K-Maxy+Min)
- 如果查询只包含(k)和左儿子,返回 (min{ ext{左儿子的}Min+K- ext{左儿子的}Maxy,V+K-k,向右儿子递归})
(看不懂请翻至约定
- 如果查询只包含左儿子,向左儿子递归
- 额,如果是FHQ-Treap,直接拆开就好。
-
最后加(n)输出
-
结尾
-
无需担心,我的代码长度只有99行而已
(然调了3h -
平衡树的好入门题
(注意细节的好入门题 -
完结撒花*★,°*:.☆( ̄▽ ̄)/$:*.°★*
-
以及,我奇丑无比的代码
#include<ctime> #include<cstdio> #include<cstdlib> #include<algorithm> using namespace std; int n,m,b[200010][5],last,root; struct r{ int l,p; }a[400010]; struct tree{ int s[2],k,v,hp,f,may,min; //注意,检测到Treap,具有随机性的平衡树,常数小,潜力不可估量(雾 }t[200010]; bool comp(r x,r y){ return(b[x.l][x.p*2]<b[y.l][y.p*2]||(b[x.l][x.p*2]==b[y.l][y.p*2]&&b[x.l][x.p*2+1]<b[y.l][y.p*2+1])); //先x后y,这也是一个坑点 } void read(int &x){ char c=getchar(); for(;c<33;c=getchar()); for(x=0;(c>47)&&(c<58);x=x*10+c-48,c=getchar()); } int newp(int f,int k,int v){ ++last; t[last].may=t[last].k=k; t[last].min=t[last].v=v; t[last].f=f; t[last].hp=rand()%10000*10000+rand()%10000; //一个生成大随机数的好办法 return(last); } int fs(int x){ return(t[t[x].f].s[1]==x); //左儿子还是右儿子,这是个问题 } void update(int now){ t[now].may=max(t[now].k,t[t[now].s[1]].may); //may即Maxy t[now].min=t[now].v+t[now].may-t[now].k; if(t[now].s[0]){ //如果有左儿子 t[now].min=min(t[now].min,t[t[now].s[0]].min+t[now].may-t[t[now].s[0]].may); } if(t[now].s[1]){ //如果有右儿子 t[now].min=min(t[now].min,t[t[now].s[1]].min); } } void fix(int now){ //特殊能力:随机重组3级,目前出现的多种组合方式减少了程序运行的时间(大雾 while(t[now].f&&t[now].hp<t[t[now].f].hp){ int fa=t[now].f,nfs=fs(now); if(t[fa].f){ t[t[fa].f].s[fs(fa)]=now; } t[now].f=t[fa].f; t[t[now].s[1-nfs]].f=fa; t[fa].s[nfs]=t[now].s[1-nfs]; t[fa].f=now; t[now].s[1-nfs]=fa; update(fa); } if(!t[now].f){ root=now; } for(;now;update(now),now=t[now].f); } void add(int root,int k,int v){ for(;t[root].s[t[root].k<=k];root=t[root].s[t[root].k<=k]); t[root].s[t[root].k<=k]=newp(root,k,v); fix(last); } int call(int root,int k){ if(t[root].may<=k){ return(t[root].min+k-t[root].may); //全部包含 } if(t[root].k<=k){ return(min(k-t[root].k+t[root].v,min(t[t[root].s[0]].min+k-t[t[root].s[0]].may,call(t[root].s[1],k)))); //包含k }else{ return(call(t[root].s[0],k)); //不包含k } } int main(){ freopen("boards.in","r",stdin); freopen("boards.out","w",stdout); srand(time(0)); read(n);read(m); for(int i=1;i<=m;++i){ read(b[i][0]);read(b[i][1]);read(b[i][2]);read(b[i][3]); a[i*2-1].l=a[i*2].l=i; a[i*2-1].p=0; a[i*2].p=1; } sort(a+1,a+m*2+1,comp); root=newp(0,0,0); for(int i=1;i<=m*2;++i){ if(a[i].p){ add(root,b[a[i].l][3],b[a[i].l][4]); }else{ b[a[i].l][4]=call(root,b[a[i].l][1])-b[a[i].l][2]+b[a[i].l][0]; //神奇的v } } printf("%d",n+call(root,n)); //完结撒输出 fclose(stdin); fclose(stdout); return(0); }