最长公共子序列算法问题代码(使用JavaScript实现)

问题描述

问题描述

题目描述:求得两个数组的最长公共子序列.子序列不要求是连续的.但是要求是有的(增序).

比如字符串1：['B','D','C','A','B','A'];字符串2：['A','B','C','B','D''A','B'].

则这两个字符串的最长公共子序列长度为4，最长公共子序列是：BCBA

• 这是一个动态规划的题目。对于可用动态规划求解的问题，一般有两个特征：
  • 最优子结构；
  • 重叠子问题:

问题推理

具体分析 : 王陸.

问题抽象

• 设c[i,j]为:x[1,i],y[1,j]的最长公共子序列长度.
  • 如果 x[i] == y[j].那么c[i][j] == (x[1,i-1],y[1,j-1]) +1
  • 如果 x[i] != y[j].那么 c[i][j] == max( (x[1,i-1],y[1,j]) || (x[1,i],y[1,j-1]) )
• 回溯表的记录是如果left/top/left_top表示当前元素的最优质是使用的之前的哪一个子元素.
  个人感觉动态规划就是把主问题的所有子问题穷尽求出最优解.把这些解放到一张里.个人感觉动态规划一般用于求最值的情况下.

我们思考的时候是要从最底层的问题层层递进的思考.从最简单的事情开始推理.

图示

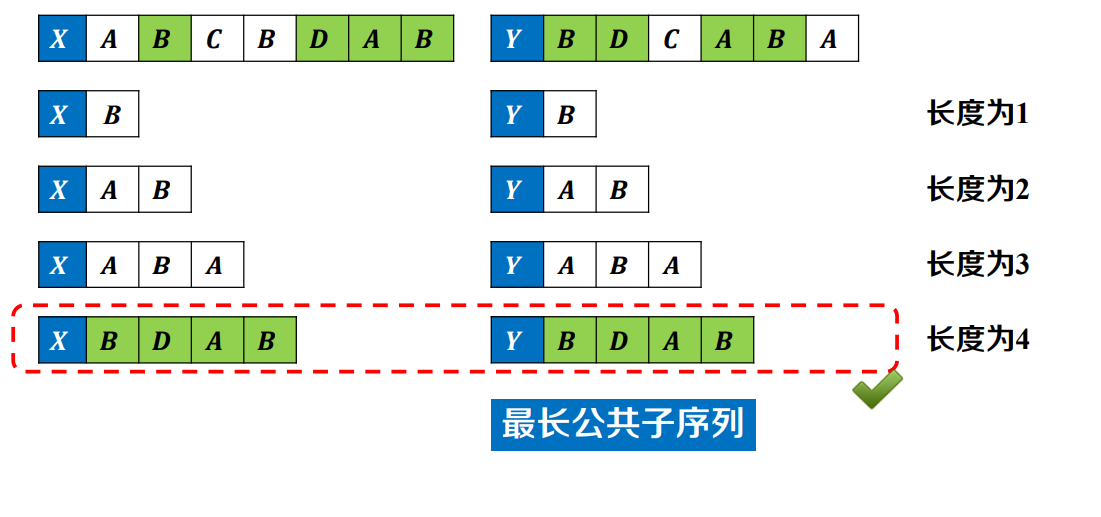
代码实现:动态规划

代码实现

 let list_a = ['A', 'B', 'C', 'B', 'D', 'A', 'B']; //序列一
        let list_b = ['B', 'D', 'C', 'A', 'B', 'A'];//序列二


        let table_dp = []; // 记录各种情况的动态表
        for (var i = 0; i <= list_a.length; i++) { // i是y轴
            table_dp[i] = [];
            for (var j = 0; j <= list_b.length; j++) { // j是x轴
                table_dp[i][j] = 0;
            }
        }
        // table_dp 二维空数组生成完毕.

        let table_rec = new Array();//回溯表
        for (let i = 0; i < list_a.length; i++) {
            table_rec[i] = [];
            for (let j = 0; j < list_b.length; j++) {
                table_rec[i][j] = null;
            }
        }
        // table_rec 二维空数组生成完毕.



        // 动态规划代码开始
        for (let i = 1; i <= list_a.length; i++) { // x==0 || y==0 的情况下,均为0.所以从1开始.设置从1开始也是为了好查表.

            for (j = 1; j <= list_b.length; j++) {

                if (list_a[i - 1] === list_b[j - 1]) { // 两个数组是要从下表为0开始遍历数据的
                    table_dp[i][j] = table_dp[i - 1][j - 1] + 1;
                    table_rec[i - 1][j - 1] = 'left_top';
                } else {

                    let max_num;
                    if (table_dp[i - 1][j] > table_dp[i][j - 1]) {
                        max_num = table_dp[i - 1][j];
                        table_rec[i - 1][j - 1] = 'top';
                    }else {
                        max_num = table_dp[i][j - 1];
                        table_rec[i - 1][j - 1] = 'left';
                    }

                    table_dp[i][j] = max_num;
                }
            }
        }
        // 动态规划代码结束

循环回溯

        // 使用while回溯
        let result = [];// 记录结果(倒序).
        x_axis_length = table_rec[0].length - 1;//二维数组x轴.
        y_axis_length = table_rec.length - 1;//二维数组y轴

        while (x_axis_length >= 0 && y_axis_length >= 0) {
            if (table_rec[y_axis_length][x_axis_length] == 'left_top') {
                result.push(list_a[y_axis_length])
                x_axis_length -= 1;
                y_axis_length -= 1;
            } else if (table_rec[y_axis_length][x_axis_length] == 'top') {
                y_axis_length -= 1;
            } else {
                x_axis_length -= 1;
            }

        }
        // 使用while结束

递归回溯

        // 使用递归回溯
        let x_axis_length_ = table_rec[0].length - 1;//二维数组x轴
        let y_axis_length_ = table_rec.length - 1;//二维数组y轴
        const result_recursion = [] // 记录结果(倒序).

        function recursion_rec(rec_list, dp_list, x_axis, y_axis) {

            if (x_axis < 0 || y_axis < 0) {
                return 0;
            }
            if (rec_list[y_axis][x_axis] == 'left_top') {
                result_recursion.push(list_a[y_axis]);
                recursion_rec(rec_list, dp_list, x_axis - 1, y_axis - 1);
            } else if (rec_list[y_axis][x_axis] == 'left') {
                recursion_rec(rec_list, dp_list, x_axis - 1, y_axis);
            } else {
                recursion_rec(rec_list, dp_list, x_axis, y_axis - 1);
            }

        }
        // 使用递归结束

        recursion_rec(table_rec, table_dp, x_axis_length_, y_axis_length_)

        // 打印结果      
        console.log(table_dp, table_rec)
        console.log(result);
        console.log(result_recursion)
  

参考

• 王陸.