CF528D Fuzzy Search (生成函数+FFT)

题目传送门

题目大意：给你两个只包含A,G,C,T的字符串$S$,$T$，$S$长$T$短，按照如下图方式匹配 解释不明白直接上图

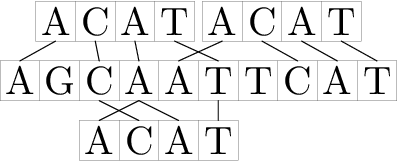
能容错的距离不超过$K$，求能$T$被匹配上的次数

$S$串同一个位置可以被$T$的不同位置匹配多次

对4种字符分别处理，假设我们现在只讨论字符A

对于字符串AGCAATTCAT，字符A的生成函数就是1001100010

题目要求距离不超过K就能匹配，把周围距离不超过$K$的位置都变成1，形成一个新串$S'$

$S$  1001100010

$S'$ 1111110111

只要$T$和$S'$的某个子串匹配时，子串中1的个数 不少于 $T$串中1的个数，就表明$T$串能被匹配上

把$T$串反转，再进行卷积，每一位都分4钟情况讨论即可

#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define N1 (1<<19)
#define il inline
#define dd double
#define ld long double
#define ll long long
using namespace std;

int gint()
{
    int ret=0,fh=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')fh=-1;c=getchar();}
    while(c>='0'&&c<='9'){ret=ret*10+c-'0';c=getchar();}
    return ret*fh;
}
int idx(char c)
{
    if(c=='A') return 0;
    if(c=='C') return 1;
    if(c=='G') return 2;
    if(c=='T') return 3;
}
const int inf=0x3f3f3f3f;

namespace FFT{

const dd pi=acos(-1);
struct cp{
dd x,y;
friend cp operator + (const cp &s1,const cp &s2){ return (cp){s1.x+s2.x,s1.y+s2.y}; }
friend cp operator - (const cp &s1,const cp &s2){ return (cp){s1.x-s2.x,s1.y-s2.y}; }
friend cp operator * (const cp &s1,const cp &s2){ return (cp){s1.x*s2.x-s1.y*s2.y,s1.y*s2.x+s1.x*s2.y}; }
}a[N1],b[N1],c[N1];
int r[N1];
void FFT(cp *s,int len,int type)
{
    int i,j,k; cp wn,w,t;
    for(i=0;i<len;i++) if(i<r[i]) swap(s[i],s[r[i]]);
    for(k=2;k<=len;k<<=1)
    {
        wn=(cp){cos(2.0*type*pi/k),sin(2.0*type*pi/k)};
        for(i=0;i<len;i+=k)
        {
            w=(cp){1,0};
            for(j=0;j<(k>>1);j++,w=w*wn)
            {
                t=w*s[i+j+(k>>1)];
                s[i+j+(k>>1)]=s[i+j]-t;
                s[i+j]=s[i+j]+t;
            }
        }
    }
}
void Main(int len,int L)
{
    int i;
    for(i=0;i<len;i++) r[i]=(r[i>>1]>>1)|((i&1)<<(L-1));
    FFT(a,len,1); FFT(b,len,1);
    for(i=0;i<len;i++) c[i]=a[i]*b[i];
    FFT(c,len,-1);
    for(i=0;i<len;i++) c[i].x/=len;
}
void init()
{
    memset(a,0,sizeof(a));
    memset(b,0,sizeof(b));
}

};
using FFT::a; using FFT::b; using FFT::c;

int s[N1],t[N1],nt[N1],n,m,K,len,L;
char S[N1],T[N1];
void solve(int p)
{
    FFT::init();
    int i,j,k,num=0;
    for(i=0,k=0;i<n;i++) if(s[i]==p) 
        for(k=max(k,i-K);k<=min(n,i+K);k++) a[k].x=1;
    for(i=n-1,k=n-1;i;i--) if(s[i]==p) 
        for(k=min(k,i+K);k>=max(0,i-K);k--) a[k].x=1;
    for(i=0;i<m;i++) if(t[i]==p) b[m-i-1].x=1,num++;
    FFT::Main(len,L);
    for(i=0;i<n;i++) if((int)(c[i].x+0.1)<num) nt[i]=1;
}

int main()
{
    int i,j,ans=0; 
    scanf("%d%d%d",&n,&m,&K);
    scanf("%s",S); scanf("%s",T);
    for(i=0;i<n;i++) s[i]=idx(S[i]);
    for(i=0;i<m;i++) t[i]=idx(T[i]);
    for(len=1,L=0;len<(n+m-1);len<<=1,L++);
    solve(0);
    solve(1);
    solve(2);
    solve(3);
    for(i=0;i<n;i++) if(!nt[i]) ans++;
    printf("%d
",ans);
    return 0;

}