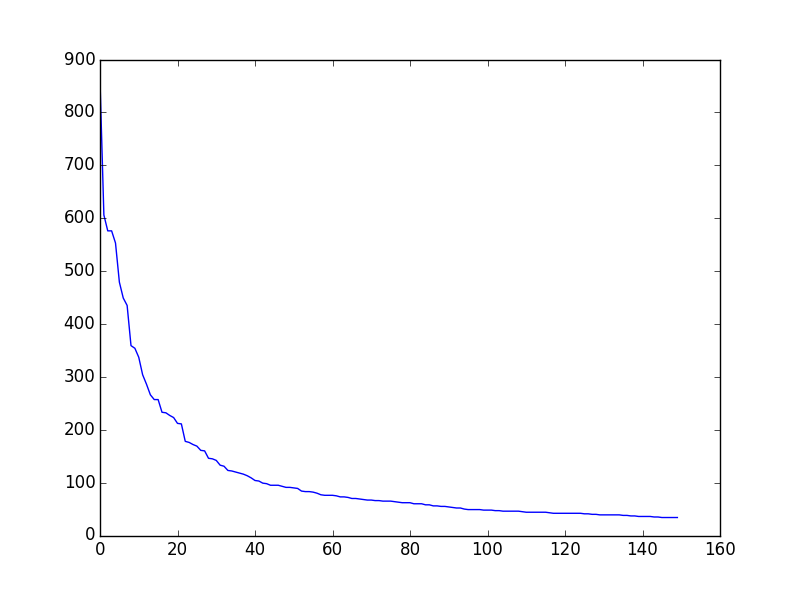
Let f(w) be the frequency of a word w in free text. Suppose that all the words of a text are ranked according to their frequency, with the most frequent word first. Zipf’s Law states that the frequency of a word type is inversely proportional to its rank (i.e., f × r = k, for some constant k). For example, the 50th most common word type should occur three times as frequently as the 150th most common word type.
a. Write a function to process a large text and plot word frequency against word rank using pylab.plot. Do you confirm Zipf’s law? (Hint: it helps to use a logarithmic scale.) What is going on at the extreme ends of the plotted line?
b. Generate random text, e.g., using random.choice("abcdefg "), taking care to include the space character. You will need to import random first. Use the string concatenation operator to accumulate characters into a (very) long string. Then tokenize this string, generate the Zipf plot as before, and compare the two plots. What do you make of Zipf’s Law in the light of this?
1 from nltk.corpus import gutenberg as gb 2 3 def validate_zipf(text,ranklimit): 4 fdist=nltk.FreqDist([w for w in text if w.isalpha()]) 5 x=range(ranklimit) 6 freq=[] 7 for key in fdist.keys(): 8 freq.append(fdist[key]) 9 y=sorted(freq,reverse=True)[:ranklimit] 10 pylab.plot(x,y) 11 12 def test(): 13 text=gb.words(fileids=['shakespeare-hamlet.txt']) 14 validate_zipf(text,150) 15
运行的结果为: