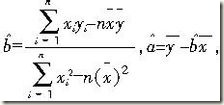回归直线方程

回归直线方程

线性回归方程的公式

一个简单实现代码

           

//************************************

// 函数名称: GetLineEquationDouble0

// 函数说明: 求线性回归方程

// 参    数:

//           const SPoint inPoint[MAX_PLATE_HEIGHT]     [in]    数据点

//           const int length                           [in]    点的数量

//           double * k                                 [out]   直线斜率

//           double * b                                 [out]   直线截距

// 返回值: byte

//************************************

byte GetLineParam(const SPoint *inPoint,constint length,double*k,double*b)

{

    int i=0;

    int sumX=0, sumY=0;

    double  xavg=0, yavg=0;

    int   sumXX =0;

    int sumXY =0;

    int tempK1 =0;

    double tempK =0;

    double tempB =0;

    if(length ==0)

    {

        *k =0;

        *b =0;

        return1;

    }

    sumX =0;

    sumY =0;

    sumXX =0;

    sumXY =0;

    for(i=0; i<length; i++)

    {

        sumX += inPoint[i].x;

        sumY += inPoint[i].y;

        sumXX += inPoint[i].x * inPoint[i].x;

        sumXY += inPoint[i].x * inPoint[i].y;

    }

    xavg = sumX / length;

    yavg = sumY / length;

    tempK1 = sumXX - length * xavg * xavg;

   

    if(tempK1 ==0)

    {

        *k =0;

        *b =0;

        return1;

    }

    tempK =(sumXY - length * xavg * yavg)/ tempK1;

    tempB = yavg - tempK *  xavg;

    *k = tempK;

    *b = tempB;

    return1;

}

一个网上看的例子

某产品广告支出x万元,与销售额y万元之间有如下数据x=2,4,5,6,8y=30,40,60,50,70(1)求回归直线方程

(1)设回归线性方程为：y=bx+a
x的平均值=（2+4+5+6+8）/5=5
y的平均值=（30+40+60+50+70）/5=50
∑xi^2=2^2+4^2+5^2+6^2+8^2=145
∑xiyi=2*30+4*40+5*60+6*50+8*70=1380
根据公式：b=（1380-5*5*50）/(145-5*5^2)=6.5
                 a=50-6.5*5=17.5
则回归线性直线方程为：y=6.5x+17.5

 

 

简单的证明

 

用最小二乘法估计参数b ,分别求对a、b的偏导数并令它们等于零，得方程组并求解.

 

假设线性回归方程为： y=ax+b (1) 
a,b为回归系数,要用观测数据(x1,x2,...,xn和y1,y2,...,yn)确定之.
为此构造 Q(a,b)=Σ(i=1->n)[yi-(axi+b)]^2 (2)
使Q(a,b)取最小值的a,b为所求.
令： ∂Q/∂a= 2Σ(i=1->n)[yi-(axi+b)](-xi)= 0 (3)
∂Q/∂b= 2Σ(i=1->n)[yi-(axi+b)] = 0 (4)
根据(3)、(4)解出a ,b就确定了回归方程（1）：
a Σ (Xi)² + b Σ Xi = Σ Xi Yi (5)
a Σ Xi + b n = Σ Yi (6)
由(5)(6)解出a,b便是,其中化简过程要用到Σ(i=1->n) (xi)  =  n T (T为X数据的均值)