AtCoder Beginner Contest 078 C HSI

虽说这是个水题，但是我做了大概有一个小时吧，才找到规律，刚学概率，还不大会做题。
找到规律后，又想了想，才想到推导过程。
思路：想要知道花费的时间，就要知道提交的次数，我在这里是计算的提交次数的期望，然后乘的花费的时间。
Takahashi 不停的提交，直到通过所有测试为止。令X是随机变量，他等于在样本空间中的一个元素中的提交次数。
即，如果一次提交就全过了，X=1，如果提交了两次，X=2。

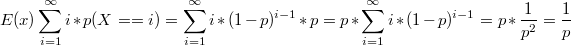
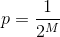
算出来提交次数的期望，乘上时间，就是结果了。
这个公式是我从《离散数学及其应用》上看到的，在409页。这本书我在图书馆看到有两本，一厚一薄，我的这本是特别厚的那本，跟个大砖头似的。
不会插入latex，只好弄成图片了，顺便保存下latex :E(x)sum_{i=1}^{{infty}i*p(X==i)=sum_{i=1}}{infty}i(1-p)^{{i-1}*p=p*sum_{i=1}}{infty}i(1-p)^{i-1}=p*frac{1}{p}

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

int main()
{
    LL n,m;
    cin >> n >> m;
    LL num = 1LL<<m;
    cout << num*m*1900+num*(n-m)*100 << endl;
    return 0;
}