上图:
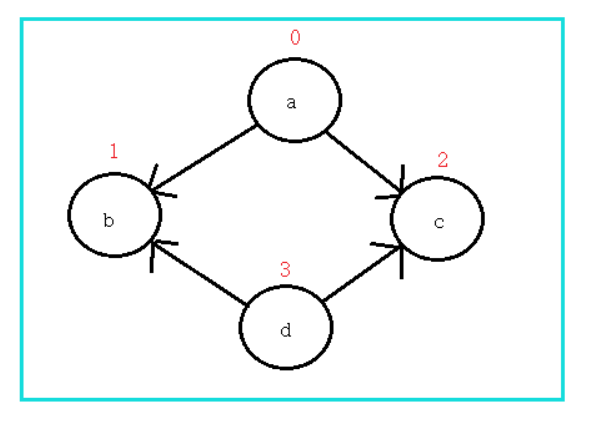
上码:
1 #include <iostream>
2 #include <queue>
3 using namespace std;
4 const int MAXSIZE = 10; //最大顶点数
5
6 template<class T>
7 class MGraph
8 {
9 public:
10 MGraph(){}
11 MGraph(T a[], int n, int e);
12 ~MGraph(){}
13 T GetVex(int i); //取某序号下顶点的数据信息
14 void PutVex(int i, T value); //将序号为i的顶点的数据域置为value
15 void InsertVex(T value); //插入结点
16 void DeleteVex(int i); //删除某序号下结点
17 void InsertArc(int i, int j); //插入一条边,给出关联顶点序号
18 void DeleteArc(int i, int j); //删除一条边,给出关联顶点序号
19 void DFSTraverse(int v);
20 void BFSTraverse(int v);
21 private:
22 T vertex[MAXSIZE]; //存放顶点数据的数组
23 int arc[MAXSIZE][MAXSIZE]; //邻接矩阵
24 int vertexNum, arcNum; //顶点数,弧数
25 int visited[MAXSIZE];
26 };
27
28 int main()
29 {
30 char a[4] = { 'a','b','c','d' };
31 MGraph<char> mg(a, 4, 4);
32 mg.DFSTraverse(0);
33 system("pause");
34 return 0;
35 }
36
37 template<class T>
38 MGraph<T>::MGraph(T a[], int n, int e)
39 {
40 vertexNum = n;
41 arcNum = e;
42 for (int i = 0; i < MAXSIZE; i++)
43 for (int j = 0; j < MAXSIZE; j++)
44 arc[i][j] = 0;
45 for (int i = 0; i < MAXSIZE; i++)
46 visited[i] = 0;
47
48 for (int i = 0; i < vertexNum; i++)
49 vertex[i] = a[i];
50 int c, b;
51 for (int i = 0; i < arcNum; i++)
52 {
53 cin >> c >> b;
54 arc[c][b] = 1; //有向图,对角线初始为0
55 }
56 }
57
58 template<class T>
59 T MGraph<T>::GetVex(int i)
60 {
61 if (i < 0 || i >= vertexNum) {
62 throw"结点不存在";
63 }
64 else
65 return vertex[i];
66 }
67
68 template<class T>
69 void MGraph<T>::PutVex(int i, T value)
70 {
71 if (i < 0 || i >= vertexNum) {
72 throw"结点不存在";
73 }
74 else
75 {
76 vertex[i] = value;
77 }
78 }
79
80 template<class T>
81 void MGraph<T>::InsertVex(T value)
82 {
83 for (int i = 0; i < vertexNum; i++)
84 {
85 if (vertex[i] == value) {
86 cout << "结点已存在" << endl;
87 return;
88 }
89 }
90 if (MAXSIZE == vertexNum) {
91 cout << "数组已满,溢出" << endl;
92 return;
93 }
94 vertex[vertexNum++] = value;
95 }
96
97 template<class T>
98 void MGraph<T>::DeleteVex(int i)
99 {
100 if (i < 0 || i >= vertexNum) {
101 throw"结点不存在";
102 }
103 if (i == vertexNum - 1)
104 {
105 for (int j = 0; j < vertexNum; j++)
106 {
107 arc[j][i] = 0;
108 arc[i][j] = 0;
109 }
110 vertexNum--;
111 return;
112 }
113 for (int j = 0; j < vertexNum; j++)
114 {
115 arc[i][j] = arc[vertexNum - 1][j];
116 arc[j][i] = arc[j][vertexNum - 1];
117 }
118 vertexNum--;
119 }
120
121 template<class T>
122 void MGraph<T>::InsertArc(int i, int j)
123 {
124 if (i < 0 || i >= vertexNum&&j < 0 || j >= vertexNum)
125 {
126 cout << "结点不存在" << endl;
127 return;
128 }
129 if (arc[i][j]) {
130 cout << "弧已存在" << endl;
131 return;
132 }
133 else {
134 arc[i][j] = 1;
135 arcNum++;
136 }
137 }
138
139 template<class T>
140 void MGraph<T>::DeleteArc(int i, int j)
141 {
142 if (i < 0 || i >= vertexNum&&j < 0 || j >= vertexNum)
143 {
144 cout << "结点不存在" << endl;
145 return;
146 }
147 if (arc[i][j])
148 {
149 arc[i][j] = 0;
150 arcNum--;
151 }
152 else {
153 cout << "弧不存在" << endl;
154 }
155 }
156
157 template<class T>
158 void MGraph<T>::DFSTraverse(int v)
159 {
160 if (v >= 0 && v < vertexNum)
161 {
162 cout << vertex[v] << ' ';
163 visited[v] = 1;
164 for (int i = 0; i < vertexNum; i++) {
165 if (arc[v][i] && !visited[i]) {
166 DFSTraverse(i);
167 }
168 }
169 }
170 }
171
172 template<class T>
173 void MGraph<T>::BFSTraverse(int v)
174 {
175 if (v < 0 || v >= vertexNum)
176 return;
177
178 queue<int> Qu;
179 int visited[MAXSIZE];
180 for (int i = 0; i < MAXSIZE; i++)
181 visited[i] = 0;
182
183 cout << vertex[v] << ' ';
184 Qu.push(v);
185 visited[v] = 1;
186 while (!Qu.empty()) {
187 int r = Qu.front();
188 Qu.pop();
189 for(int i=0; i<vertexNum; i++)
190 if (arc[r][i] && !visited[i]) {
191 cout << vertex[i] << ' ';
192 Qu.push(i);
193 visited[i] = 1;
194 }
195 }
196 }
不足之处:
删除某结点可能导致结点序号改变;函数入口应传递结点信息而非序号