下面是一道题目:
在一个排序了的整数数组中(包含100万整数),寻找某一个特定的数。二分搜索、先构建二叉树再利用这棵树作为索引进行搜索,这两种搜索的时间复杂度都是logN。 什么时候该用第一种,什么时候该用第二种?
看到这道题目考察的是二分查找和二叉树查找的比较和优劣选择的关系。
(1)这里数组是一个100万的有序数组。
(2)两者的时间的复杂度相同为logN
关于二分查找和二叉树的理解:
(1)二分查找即折半查找,优点是比较次数少,查找速度快,平均性能好;其缺点是要求待查表为有序表,且插入删除困难
(2)二叉查找树,它或者是一棵空树,或者若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
两者明显的区别是二分查找速度快删除和插入困难,二对于建立的二叉树索引来说,他的插入和删除是相对较快的。为什么会出现
这两者的差别其实底层更多的考虑的是数据的存储结构:
顺序存储和链式存储的概念
(1)从空间性能,顺序存储会对空间资源做到百分之百的利用,而链式存储对对空间的利用不是百分之百,因为存储了指针,不是真正的数据
(2)从时间性能上来讲读取速度的话顺序存储更优,插入和删除操作链式存储更优,链式存储只需要移动指针,不需要移动元素。
所以这个问题什么时候采用二分什么时候采用二叉索引
(1)如果我们的数据是不进行频繁变化且是有序,而且查询相对较多的情况下采用二分查找
(2)我们的数据是频繁变化的考虑到后面的数据扩容的情况下,我们考虑采用二叉索引的方式,但是这种会有一点空间资源的牺牲。
题目的意思是什么时候采用哪种方案。这里条件限定死了。首先数组固定有序,然后两者的复杂度都是logn,也就是两者的时间复杂度算法是相同的,这个时候就考虑采用
二分查找的算法。这样在进行频繁查找的情况下效果会很好。
至于二叉查找的算法,因为从时间复杂度的算法上面考虑。两者的算法如下:
(1) 二分查找时间复杂度算法:
第一次 N/2
...
第k次 N/2^k
最坏的情况下第k次才找到,此时只剩一个数据,长度为1。
即 N/2^k = 1
查找次数 k=log(N)。
(2)对于二叉查找的时间复杂度算法理想状态下,他的时间复杂度和二分查找是相同的都是log(N)。
但是, 最差情况为所有数据全部在一端时(链表无索引,需要一个一个搜索),如图:
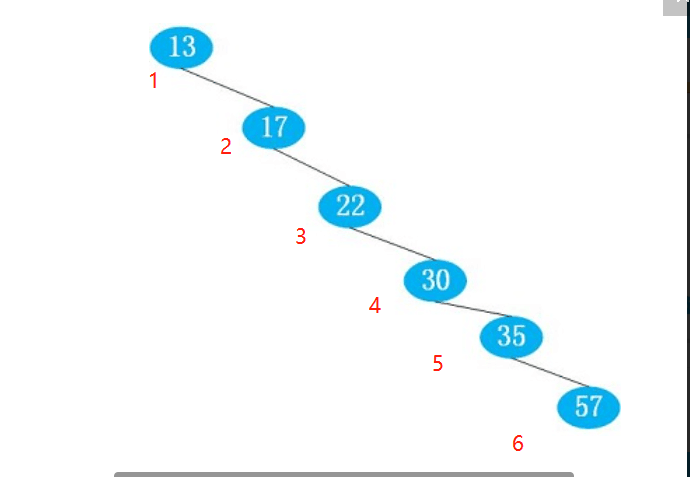
这个时候的时间复杂度就是相当于一个一个去匹配,然后找到我们想要的那个数。这个时候的时间复杂度就变成了O(n),不在是理想状态下的O(logn)