luogu题解 CF767C 【Garland】

Part.1

一开始完全没有思路,想了一下，如果是分成两棵树，那就好做多了，首先想到的是统计一下以当前节点为根的子树的权值和，如果和为(sum imesfrac{1}{2})，那么我们就找到了一个解。考虑我们也类似地记录一个(siz)表示以当前节点为根的子树的权值和，只要为(sum imesfrac{1}{3})，它就可能是解的一个。

Part.2

我们在一遍(dfs)后可以找出可能很多是(sum imesfrac{1}{3})的解，那么我们应该怎么选择呢？很容易想到，我们应该找到(LCA)不同的两个点，我们就找到了一组解。

Part.3

上述解法实际上是存在问题的（想一想，为什么）

我们考虑类似下面的一棵树：

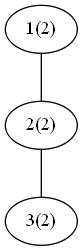
很显然这棵树上子树权值和为(sum imesfrac{1}{3})只有三号节点，但我们能不能把他分成三棵树呢？很显然是可以的（每个节点都分成一棵树），我们的解法应进一步考虑。考虑二号节点，它的权值和是(sum imesfrac{2}{3})，那我们怎么处理呢？难道要把所有的(sum imesfrac{1}{3})与(sum imesfrac{2}{3})算出来，然后再一一匹配吗？

我们考虑另一种解法。(dfs)的特点是要在处理完儿子后才会处理当前节点，考虑儿子中有一个(sum imesfrac{1}{3})，如果我们吧儿子的(sum imesfrac{1}{3})变成(0)，那么它自身也变成了(sum imesfrac{1}{3})，我们此时只用一个数组统计为(sum imesfrac{1}{3})的节点就ok了，那么如果有两个儿子都是(sum imesfrac{1}{3})呢？我们一定会先处理儿子，那么儿子都被统计了，自然就找到答案了。

我们只用输出找到的前两个答案即可。（这两个答案一定是我们上述提到的两种关系）

最后奉上高清无码的代码：

#include <cstdio>
#include <iostream>
using namespace std;
const int maxn=1e6+5;

struct edge
{
    int v,nxt;
}e[maxn<<1];
int head[maxn],kt;
int t[maxn],rt,n;
int ans[10],tot;
int sum;
template<typename T>
inline void read(T &x)
{
    char c;int f=1;
    while(!isdigit(c=getchar())) (c=='-')&&(f=-1);
    x=c^48;
    while(isdigit(c=getchar())) x=(x<<1)+(x<<3)+(c^48);
    x*=f;
}

inline void add(int u,int v) {e[++kt]=(edge){v,head[u]};head[u]=kt;}

void dfs(int u,int f)
{
    for(int i=head[u];i;i=e[i].nxt)
    if(e[i].v!=f)
    {
        dfs(e[i].v,u);
        t[u]+=t[e[i].v]; 
    }
    if(t[u]==sum/3)
        ans[++tot]=u,t[u]=0;
}

int main()
{
    int x;
    read(n);
    for(int i=1;i<=n;i++)
    {
        read(x);read(t[i]);
        sum+=t[i];
        if(x) add(x,i),add(i,x);
        else rt=i;
    }
    if(sum%3)
    {
        puts("-1");
        return 0;
    }
    dfs(rt,0);
    if(tot<=2) puts("-1");
    else printf("%d %d
",ans[1],ans[2]);
    return 0;
}