1、在电气和电子工程师协会IEEE 754 标准中
-
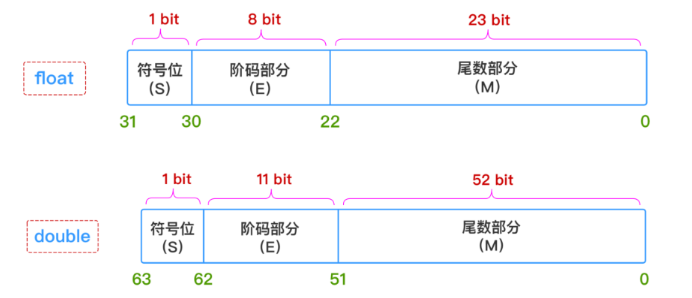
float单精度浮点数(4个字节,32位)在机器中表示:用1位表示数字的符号(正负号),8位表示指数,23位表示尾数(即小数部分)
-
double双精度浮点数(8个字节,64位):1位表示符号(正负号),11位表示指数,52位表示尾数
浮点数阶码E用“指数e的移码-1”表示,还可以用阶码E的移码(特殊的移码)+阶码E的真值(即指数)表示。
阶码的移码:假设阶码用8个二进制位表示,则该阶码的移码为 2(n-1) ,但注意这里的移码是特殊的移码,仅偏移2(n-1)-1=127 。
2、浮点数的规格化
同一浮点数表示方式不唯一(如1.5=1.01x2(0) =0.101*2(1)),所以规定当尾数不为0时,向左或向右移动小数点,使得小数点左边始终为1(即1.M的格式)。
3、单精度浮点数真值
一个规格化32位的浮点数x的真值表示为:x=(-1)(s)x(1.M)x2(e) , e=E-127 , E=e的移码-1
4、十进制到机器码
(1)0.5=(0.1)(二进制),符号位s为0,指数为e=-1,规格化后尾数为1.0
单精度浮点数尾数域(从小数点后开始)共23位,右侧以0补全,尾数域:
M=[000 0000 0000 0000 0000 0000](二进制)
阶码E:E=[-1](的移码)-1=[0111 1111](二进制)-1=[0111 1110](二进制)
或者 E=127(2(8-1)-1,特殊的移码)+(-1)(指数)=126=[0111 1110](二进制)
将符号位s,阶码E和尾数域M存放到指定位置,可得0.5的机器码为:
0.5=[0011 1111 0000 0000 0000 0000 0000 0000](二进制)
十六进制表示为:0.5=0x3f000000 (0x:表示十六进制,0011:3,1111:f,)
(2)1.5=[1.1](二进制),符号位为0,指数e=0,规格化后尾数为1.1。
尾数域M右侧以0补全:M=[100 0000 0000 0000 0000 0000](二进制)
阶码E:E=[0](的移码)-1=[10000000](二进制)-1=[01111111](二进制)
得1.5的机器码:1.5=[0011 1111 1100 0000 0000 0000 0000 0000](二进制)
十六进制表示:1.5=0x3fc00000
(3)−12.5=[−1100.1](二进制) ,符号位S为1,指数e为3,规格化后尾数为1.1001,
尾数域M右侧以0补全:
M=[100 1000 0000 0000 0000 0000] (二进制)
阶码E:
E=[3](的移码)−1=[1000 0011](二进制)−1=[1000 0010](二进制)
即-12.5的机器码:
−12.5=[1100 0001 0100 1000 0000 0000 0000 0000](二进制)
十六进制表示:-12.5=0xc1480000 。
5、机器码到十进制
若某个浮点数的IEEE 754标准存储格式为0x41360000,那么其浮点数的十进制数值为多少:
0x41360000=[0 10000010 011 0110 0000 0000 0000 0000]
有上述机器码可知符号位s=0,指数e=阶码-127=1000 0010-127=130-127=3,或者阶码+1=移码,移码变换为原码求得指数 ,10000010+1=10000011(移码)=00000011(原码)=3(指数e)
尾数域为:011 0110 0000 0000 0000 0000,第一个0的左边隐藏了一个1,即尾数1.M=1.011 0110 0000 0000 0000 0000
于是:x=(-1)(s)x1.Mx2(e)=+(1.011011)x2(3)=+1011.011=(11.375)(十进制)
6、浮点数的特殊情况
(1)0的表示(32位为例)
如果阶码E=0,且尾数M是0,则这个数的真值为+0或-0
+0机器码为:0 00000000 000 0000 0000 0000 0000 0000
-0机器码为:1 00000000 000 0000 0000 0000 0000 0000
浮点数不能精确表示0,而是以很小的数来近似表示0,以32位单精度浮点数为例:
x=(-1)(s)x(1.M)x2(e) , e=E-127
+0的机器码对应的真值为:1.0x2^(-127)
-0的机器码对应的真值为: -1.0x2^(-127)
(2) ±∞的表示(32位为例)
如果阶码E=255,且尾数M是0,则这个数的真值为+∞或-∞
+∞的机器码为:0 11111111 000 0000 0000 0000 0000 0000
-∞的机器吗为:1 11111111 000 0000 0000 0000 0000 0000
x=(-1)(s)x(1.M)x2(e) , e=E-127
+∞的机器码对应真值为:1.0x2^(128)
-∞的机器码对应真值为:-1.0x2^(128)
7、浮点数的精度
浮点数的精度是由尾数的位数来决定的:
- 对于
float型浮点数,尾数部分23位,换算成十进制就是2^23=8388608,所以十进制精度只有6 ~ 7位; - 对于
double型浮点数,尾数部分52位,换算成十进制就是2^52 = 4503599627370496,所以十进制精度只有15 ~ 16位
例题:以下例题是在java编译环境下检测的。
1、为什么以下返的结果为true?
System.out.println(1f==0.99999999f);
//结果返回 true
分析:
1.0(十进制)=1.0(二进制)* 20
↓
0 01111111 0000000 00000000 00000000(二进制)
↓
0x3F800000(十六进制)
0.99999999(十进制)
=0.111 111 111 111 111 111 111 111110(二进制)
(猜测:浮点数的尾数只有23位,事先将第24位加一,把进位加到第23位,结果为1.0000000 00000000 00000000)
(实际上和编译器有关,当小数点后的23位全为0时,编译器就当成全0处理,即0.0000000 00000000 00000000)
=0.0000000 00000000 00000000* 20
↓
0 01111111 0000000 00000000 00000000(二进制)
↓
0x3F800000(十六进制)
原因:float型浮点数十进制精度只有6 ~ 7位,而0.99999999f小数点后有8位,超出了精度范围(猜测产生了进位)。
2、为什么以下返回的结果为`false`?
System.out.println(1f==0.9999999f);
//结果返回 false
分析:
0.9999999(十进制)
=0.1111111 11111111 111111110(二进制)
(第24位为0加一不产生进位,所以结果是小数点后23个1,最后进行规范化处理缺位补0)
=1.111111 11111111 11111110(二进制) * 2-1
↓
0 01111110 1111111 11111111 11111110(二进制)
↓
0x3F7FFFFE(十六进制)
这些只是我个人的理解,可能不是很精确,如有错误欢迎指正,相互交流共同进步!