HDU4539（状态压缩动态规划）

原题链接

算法解析

首先观察数据范围

我们发现，(n le 10)

这是状态压缩DP的典型数据范围

接着我们看本题是一个棋盘，然后一个点的放置受到其他点的限制。

那么我们可以确定本题为棋盘类型的状态压缩

显然每一行的状态是必须储存下来的

问题是，这里有m行，那么这么多数据，我们难道要全部压缩进来吗？

完全不能！

那么我们来观察一个点的状态限制

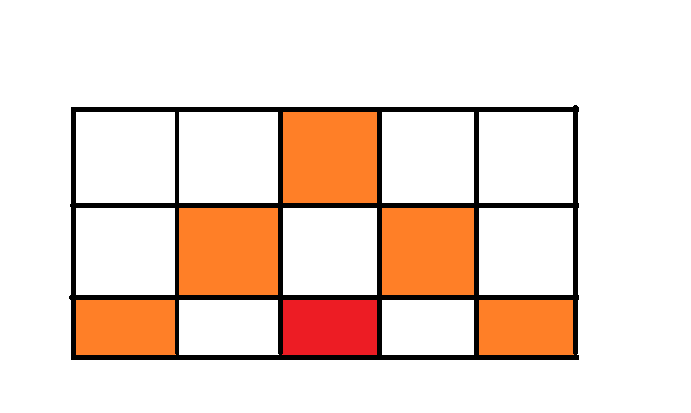
红色是我们当前放置的点，而橙色是我们不能放置的点。

根据上面的图片显示，一个点在不考虑下面摆放的前提下，我们只需要考虑上面两行的状态。

我们不妨设f[2][a][b]表示当前行，状态为a,上一行的状态为b

那么在这里，我们状态转移就是

f[i][a][b]=max(f[i][a][b],f[i-1][b][c]+cnt[a])

在这里cnt[a]表示状态为a，放置了多少个士兵

接下来我们需要考虑状态限制的具体表示：

1. 放置士兵的格子，左边2格，右边2格上不能有士兵
2. 放置士兵的格子，上面一行，左边1格，右边1格不能放置士兵
3. 放置士兵的格子，上上行不能放置士兵

然后一个状态，有10位，那么存放大小得为1024

但是根据同一行，左右2格上不能放置的规定（也就是第一条）

我们发现最后合法的状态，一共有169个状态

所以我们不妨把这些合法状态编号，然后用编号来表示对应的状态

这样可以压缩状态，保证不超内存

最后记得一点：循环枚举时候，遇到不合法的状态，直接跳过，不要浪费时间。（具体看代码实现）

易错点总结：

1. 没有考虑上上行的状态
2. 状态没有压缩好，导致MLE

代码解析

#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cstring>
using namespace std;
int f[2][220][220],cnt[210],n,m,pre[110],ok[220],qs;//其实可以用滚动数组
inline int check1(int a)
{
	bool ok1=a & (a<<2);//判断a有没有自己打自己的
	return ok1;
}
inline int check2(int a,int b)//a为这一行状态,b为上一行状态
{
	bool ok1=b & (a<<1);//来自右边的
	bool ok2=b & (a>>1);//来自左边的
	return (ok1 | ok2);
}
int count(int x)//统计这种状态下，放置点的数量
{
	int ans=0;
	while(x)
	{
		ans+=(x&1);
		x>>=1;
	}
	return ans;
}
inline void work()
{
	int ans=0;
	for(int i=1; i<=m; i++)
	{
		for(int s=0 ; s<qs; s++)//当前行
		{
			int now=ok[s];
			if (now & pre[i])//自判 &子集判断
				continue;
			for(int j=0; j<qs; j++)
			{
				int last=ok[j];
				if (last & pre[i-1])//判断状态是否自身合法，可以放置
					continue;
				if (check2(now,last))//上下对打
					continue;
				for(int k=0; k<qs; k++)
				{
					int kk=ok[k];
					if (kk & pre[i-2])//判断状态是否自身合法，可以放置
						continue;
					if (check2(last,kk))
						continue;
					if (now & kk)//自己和上上对打，很重要
						continue;
					f[i & 1][s][j]=max(f[i & 1][s][j],f[i-1 & 1][j][k]+cnt[s]);
					//f[i][j][k]当前行为i，当前行状态的代号为j，上一行状态的代号为k
				}
			}
		}
	}
	for(int i=0; i<qs; i++)
		for(int j=0; j<qs; j++)
			ans=max(ans,f[m & 1][i][j]);
	printf("%d
",ans);
}
inline void init()
{
	while(scanf("%d%d",&m,&n)!=EOF)
	{
		memset(f,0,sizeof(f));
		memset(pre,0,sizeof(pre));
		qs=0;
		for(int i=0; i<1<<n; i++)
			if(!check1(i))//找到满足自己不打自己的状态们
				ok[qs]=i,cnt[qs]=count(i),++qs;//统计子集状态
		int now=0;
		for(int i=1; i<=m; i++)
			for(int j=0; j<n; j++)
			{
				scanf("%d",&now);
				if (now==0)
					pre[i]+=(1<<j);//构造不可以放士兵的状态
			}
		work();
	}
}
signed main()
{
	init();
	return 0;
}