本篇是这个系列的最后一篇,尽管在区块链中还有很多的密码学应用,将来会必然会更多,然而笔者认为,就今天我们有限的学习时间来讲的话,任何人都应该对信息的获取做减法。思来想去,选择了“零知识证明”来作为本系列的终章。
什么是零知识证明?
wiki百科上对于零知识证明的描述是这样的:证明者可以向验证方证明他们知道X的值,但是不传达任何信息,除了他们知道X的值这件事。零知识证明的本质是通过简单地揭示它来证明某人拥有某些信息,难点在于证明这种占有而不泄露信息本身。
一个经典的例子:阿里巴巴和四十大盗的故事,阿里巴巴知道一个打开藏有宝藏的山洞的咒语,强盗抓住他,逼他说出咒语。阿里巴巴担心自己说出咒语以后会被强盗杀死,于是他对强盗提出了一个办法:你们离我弓箭能射到的距离,你们举起右手我就念咒语打开石门,你们举起左手我就念咒语关闭石门,这样的话如果我不知道咒语你们也可以直接射箭杀死我。这个方案的结果就是:阿里巴巴不用告诉强盗咒语但是证明了他知道咒语。这就是零知识证明应用的一个经典案例。
零知识证明分为交互式和非交互式,顾名思义,前者需要证明者和验证者多次交互完成证明。后者是只要证明者给出答案,后续就不需要交互,任何人都可以证明结果是否正确,但是为了不让整个过程完全由证明者把控(容易作弊),事先一般会约定一个种子,基于这个种子产生的随机序列来完成证明。
零知识证明在区块链中的应用?
就目前区块链发展中,零知识证明的应用有基于zkSNARKs的Zcash项目,有应用基于零知识证明的签名算法的Hyperledger Fabric项目,有在项目中使用Schnorr签名算法的。区块链中零知识证明的应用灵活多样,但本质上还是为了在不泄露消息的情况下完整某种证明。本文重点讲述zkSNARKs的应用。
在区块链网络中,有一个可以算作优点也可以算作缺点的地方,那就是区块链网络的透明,不可篡改。任何操作都是由共识产生的,所有节点记录了共识的结果,所以在比特币网络在任何交易都是可追溯的。也就是说A账户向B账户转账,C,D,E,F账户转账,全网都是可见的。对于现在社会而言,虽然区块链世界是通过虚拟地址来标示用户身份,但是结合ip信息,上网信息,获取一个用户的真实信息是可能的。所以zCash结合了zkSNARKs的零知识证明实现了对于交易信息的保护。
zkSNARKs 原理
zkSNARKs 是一种新兴的零知识证明方式,笔者将基于V神的介绍 (查看原文需要翻墙),结合自己的理解给读者介绍zkSNARKs的实现原理。
下图是一个zkSNARK是的整个过程:


简单的说,一次zkSNARKs的过程首先是把问题转换成R1CS的约束,在由约束转换到QAP的形式。然后在对这个QAP做一次性的约束校验。可能这句话不太明白,没关系,我们一步步往下看。
我们假设有一个函数:
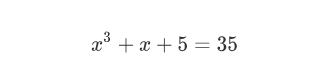
这个公式比较简单,方便后面构造QAP。我们把这个函数转换成代码:
def qeval(x)
y = x**3
return x + y + 5
有些编程基础的读者都能看明白这个函数,语法有一些不一样的地方但是都大同小异,这里不做介绍。
下面要对这个函数做的第一步操作叫做:
抹平
抹平就是把上面的代码转换成一种最简单的表达式,类似于电路的逻辑门运算,不存在多次方和多个符号运算。上面的代码抹平以后的内容为:
sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5
可以发现转换以后的效果跟之前是一模一样的,区别在于这里的运算都是简单的运算。
转R1CS
R1CS是一系列的向量构造的三元向量组<a,b,c>。假设有对这个向量组的解s,那么s满足:s·a * s·b - s·c = 0。看下图就能很好的理解这个公式:
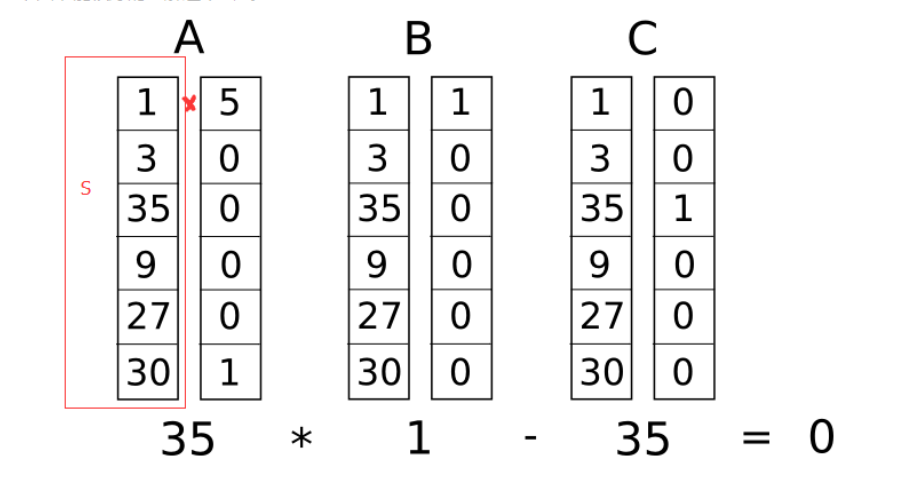

s·a就是向量s和向量a的对应元素相乘的和。
那么上面的解s就满足刚才说的公式 。上面的图向我们展示了对于我们要证明的公式的一个约束,回头再看我们第一步抹平以后的代码,接下来我们要做的就是把四行代码的每一步都转换成a,b,c向量组的方式。转换的过程要根据逻辑运算符来决定,每个向量的长度是整个逻辑运算中的变量长度,上面的逻辑运算中有五个变量,但是实际操作过程中会在每个向量中添加一个名称为one的变量。所以我们一共 有6个变量及映射的顺序如下:
one, x, ~out, sym_1, y, sym_2。
现在一次根据公式给出每一组逻辑门的向量a,b,c。
第一组:sym_1 = x * x。因为x,sym_1分别在上面定义的顺序中的第二个和第四个,所以向量中a的第二个值为1,c的第四个值为1。a和b相同。得出第一组abc向量为:
a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]
对于这一组,要满足s·a * s·b - s·c = 0,只需要解s的第二个位置是3,第四个值为9就能满足条件。当然这只是总舵满足条件的约束之一,还有很多解。
第二组:y = sym_1 * x。因为sym_1在第四个,所以a的第四个值为1,b对应x,第二个值为1,c对应y,第五个值为1。所以第二组的abc向量为:
a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]
第三组:sym_2 = y + x。这跟前面不同,这是一个加法,可以理解为是把s的第一个元素乘以a的第二个值的结果加上第五个值。所以这一组的向量为:
a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]
同样的算法,第四组为:
a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]
这个是四个带有约束条件的R1CS,他的见证者就是对这些所有输入输出还有中间变量的一组赋值:
[1, 3, 35, 9, 27, 30]。
转QAP
相较于R1CS的单一约束,读者可以想象,在零知识证明中光靠这一点就能完全证明你知道该公式的解吗?复杂一点的函数就跟我们玩数独游戏,单次的结果是有可能“蒙”对的。所以转QAP的目的就是为了同时检查所有的约束。
转QAP本质上是想要实现一个表达式能够满足所有的条件,这里利用到数学中的 拉格朗日插值法 。它能够实现把一些坐标系转换成满足条件的多项式。
这个过程其实并不复杂,只需要取出每个abc向量的每一个元素进行拉格朗日差值运算,得到一个向量组就能求出多项式。比如a:
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]
系数是按照阶数排序的,越往后越高,所以上面的多项式为:
按照同样的方法得出abc的三组多项式。

检验QAP

上面的公式结果也是一个多项式,我们的目标是确保上面的公式得出的多项式在逻辑门对应的点的位置结果是0,这样就代表所有的检查通过。为了检查多有的点,不应该去把每一个点放到公式中代入执行。这里假设:
t = A·s * B·s - C·s。基于之前运算:
A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]
所以t的结果是:
t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]
注意这里的运算都是多项式之间的运算。可以发现在x的值为1,2,3,4的时候t为0。那么A·s * B·s - C·s的多项式结果一定是z=(x - 1) * (x - 2) * (x - 3) * (x - 4)的倍数。所以做运算:
h = t / Z = [-3.666, 17.055, -3.444]
所以就有QAP的解。
这是一个非常简单的例子,但是实际中这些加减乘除的运算是在有限域中完成的。在有限域中不用担心计算中产生的误差,比如小数取整之类的,而且整个系统和椭圆曲线完美配合,保证了zkSNARKs的安全。
zkSNARKs在Zerocoin中的应用
Zerocoin做了一个创新,在交易中花费一定的货币来生成一个零币,每个零币有独特的序列号,同时所有的节点共同维护一个作废列表,所有被花费的零币的序列号记录在其中。交易被验证时使用零知识证明的方法,可以在完全不知道消耗的是哪个币的情况下验证交易是否有效。由于交易中并没有签名和地址等信息,整个交易过程中,矿工也并不知道这个零币的来源,因此也就难以对交易历史进行分析而获取用户身份。
zkSNARKs在Zerocoin中的应用是一个很复杂的过程,包括零知识需要的复杂的数学知识。为了降低理解的难度,本文将在接下来将简述zkSNARKs在Zerocoin中的应用,以便读者能够理解这个过程。
-
对于一次交易验证过程来说,可以将它拆解成一个个逻辑上的验证步骤,进而拆解成由简单算法构成的算术电路。
-
通过一系列的变换将需要验证的程序转换成验证多个多项式乘积是相等的,如证明t(x)h(x)= w(x)v(x)。
-
为了让我们的验证更快一点,验证者会首先随机验证一个S点的结果对于等式是否成立。这样的目的能够让证明过程更加高效。
-
对需要验证的公式进行同态加密(一种加密函数,对明文进行环上的加法和乘法运算再加密,与加密后对密文进行相应的运算,结果是等价的),这样的话验证者在验证的过程中无法获输入的值。
-
对于t(x)h(x)= w(x)v(x)等式都乘以一个K值,这个K是保密的。那么验证者就不知道本来的t(x),h(x),w(x),v(x)。因此信息得到保护。
除此之外,Zerocoin和Zcash都需要内置一些参数,这个参数的不泄露保证了网络的安全。Zcash团队曾经利用切尔诺贝利的核废弃产生随机数以保证加密货币的安全性。在仪式上,开发人员通过驾驶飞机,确保了恶意参与者不可能在其过程中破坏代码。此外,为了确保放射源产生真正的随机脉冲,Zcash团队成员将电池连接到他们的数据收集器上进行了比较。其结果是,在理论上,产生了一个完全随机的、私有的代码,用于构建Zcash网络系统。在zkSNARKs之后还有zkSTARKs,它解决了zkSNARKs必须依赖一个可信的系统设置的缺点,这里不做过多的介绍。
整个区块链中对于密码学的应用非常多,随着区块链的发展还会有越来越多的加密算法,共识算法被应用到区块链网络中。作为从业者应该能“知其然而知其所以然”,理解区块链背后的技术本质。
参考:
https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649