Best Time to Buy and Sell Stock
题目等级:Easy
题目描述:
Say you have an array for which the ith element is the price of a given stock on day i.
If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.
Note that you cannot sell a stock before you buy one.
Example 1:
Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Not 7-1 = 6, as selling price needs to be larger than buying price.
Example 2:
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.
题意:给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。注意不能在买入股票前卖出股票。
解题思路:
对于本题,有以下两种解法:
解法一:Brute Force暴力解法
由于限制只允许一次交易,那么一个最直观的解法就是对每一天,都依次遍历它之后的所有可能卖出的情况,记录最大值,最后进行比较得出最终结果。很显然这是一个二重循环,时间复杂度为O(n^2),空间复杂度:O(1)。
换句话说,这也就是将所有可能的买卖情况都穷举出来,然后找最大值。
public int maxProfit(int[] prices) {
//解法一:蛮力法,找到每一天后续的最大值,比较确定最大利润
//时间复杂度:O(n^2),空间复杂度:O(1)
if(prices==null || prices.length==0)
return 0;
int maxprofit=0;
for(int i=0;i<prices.length;i++){
for(int j=i+1;j<prices.length;j++){ //如果第i天买入,依次判断它之后的每一天卖出的情况
if(prices[j]-prices[i]>maxprofit)
maxprofit=prices[j]-prices[i];
}
}
return maxprofit;
}
解法二:动态规划法
暴力法需要二重循环,解法二通过动态规划使得只需要一次遍历即可找到最大值,动态规划适用于多阶段决策过程的最优化问题,明显这里就是一个决定什么时候买和卖出的阶段决策问题。
如果我们用dp[i]表示从第1天到第i天进行一笔交易能获得的最大收益,用min表示买入时的价格(最低的时候),则dp[i]=max(price[i]-min,dp[i-1]),其中maxProfit是指已经找到的最大收益。
在求出所有的dp[i]以后我们再找到其中的最大值,即为所求值,由于只需要找到最大值,因此可以合二为一,遍历的过程中顺便求最大值,因此递推公式变为:
dp[i]=max(price[i]-min,maxProfit)
由于只允许一次交易,所以要想获得最大收益,必须在价格最低的时候买入,最高的时候卖出,但是由于必须先买后卖,所以如果用波形来说,就是要找到一个波峰和波谷,波谷在波峰之前。
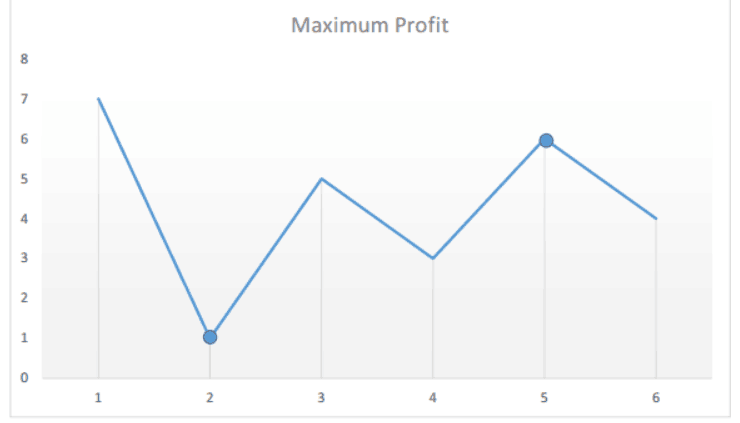
在这里,我们只需要维护一个min变量,就可以省去一层循环,代码如下:
public int maxProfit(int[] prices) {
//解法二:动态规划法:用dp[i]表示第i天卖出的收益,则dp[i]=max(price[i]-min,maxProfit)
//时间复杂度:O(n),空间复杂度:O(1)
if(prices==null || prices.length==0)
return 0;
int len=prices.length;
int maxprofit=0,min=Integer.MAX_VALUE;
for(int i=0;i<len;i++){
if(prices[i]<min) //维护一个最小值
min=prices[i];
else if(prices[i]-min>maxprofit)
maxprofit=prices[i]-min;
}
return maxprofit;
}
总结
以上两种解法实际上都比较好理解,实际上,暴力法就是我们先确定哪一天买,这样卖出的选择就需要遍历,而动态规划法,我们是先确定哪一天卖,由于题目的特点,那么买的时间就是卖之前的最小值,正好在这个遍历的过程中我们就能把这个最小值记录下来,因此得到了性能的提升。