Given some segments of rope, you are supposed to chain them into one rope. Each time you may only fold two segments into loops and chain them into one piece, as shown by the figure. The resulting chain will be treated as another segment of rope and can be folded again. After each chaining, the lengths of the original two segments will be halved.
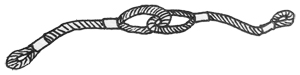
Your job is to make the longest possible rope out of N given segments.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (2). Then N positive integer lengths of the segments are given in the next line, separated by spaces. All the integers are no more than 1.
Output Specification:
For each case, print in a line the length of the longest possible rope that can be made by the given segments. The result must be rounded to the nearest integer that is no greater than the maximum length.
Sample Input:
8
10 15 12 3 4 13 1 15
Sample Output:
14题意:
给出N段绳子,要求将着N段绳子串联起来,寻找传来的策略使最后串联出来的绳子最长。两个绳子串联就是将两个绳子对折之后使其连接在一起。
思路:
最先串联的绳子对折的次数最多,所以应该将短的绳子先串联起来,这样可以保证长绳子的对折次数最少,从而保证最后的长度最长。
Code:
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 int main() { 6 int n; 7 cin >> n; 8 vector<int> v(n); 9 for (int i = 0; i < n; ++i) cin >> v[i]; 10 sort(v.begin(), v.end()); 11 double ans = v[0]; 12 for (int i = 1; i < n; ++i) { 13 ans = (ans + v[i]) / 2; 14 } 15 cout << (int)ans << endl; 16 return 0; 17 }
刚开始做的时候没有理解题意,以为可以不用将所有的绳子都串联进来就可以得到最大长度(将两个15单位长的绳子对折之后绳子的长度还是15,这样不就比14还要长了吗?),但是题目中有这样一句话“you are supposed to chain them into one rope.”,通过这句话我们可以知道题目是要我们将所有的绳子都串联起来。参考了(https://www.liuchuo.net/archives/3741)