Practice link : https://vjudge.net/problem/HDU-6832
题意: n 个点,m 条边,第 i 条边的权值是 2^i ,问每个 1 到每个 0 的最短距离之和。
即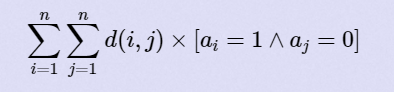
思路:首先看边的权值 是 2^i ,我们可以联想到 2^0+2^1+......+2^(n-1)< 2^n,对于第 i 条边,如果这条边连接的 u和v 是已经被前 i - 1 条边连接,则这条边可以直接抛掉。看到这个选边的过程,也就是最小生成树kruskal发的选边原则,因此我们可以跑一遍最小生成树来确认整张图,也就是一棵树,在这个棵树上每个01点对的路径只有一条且保证是最短路径。接下来我们只需要确定每一条边所使用的次数即可。观察一幅图,对于任意一条边,它的使用次数就是 这条边上方的 1 的数量 * 下方 0 的数量 +上方的 0 的数量 * 下方的 1 的数量。
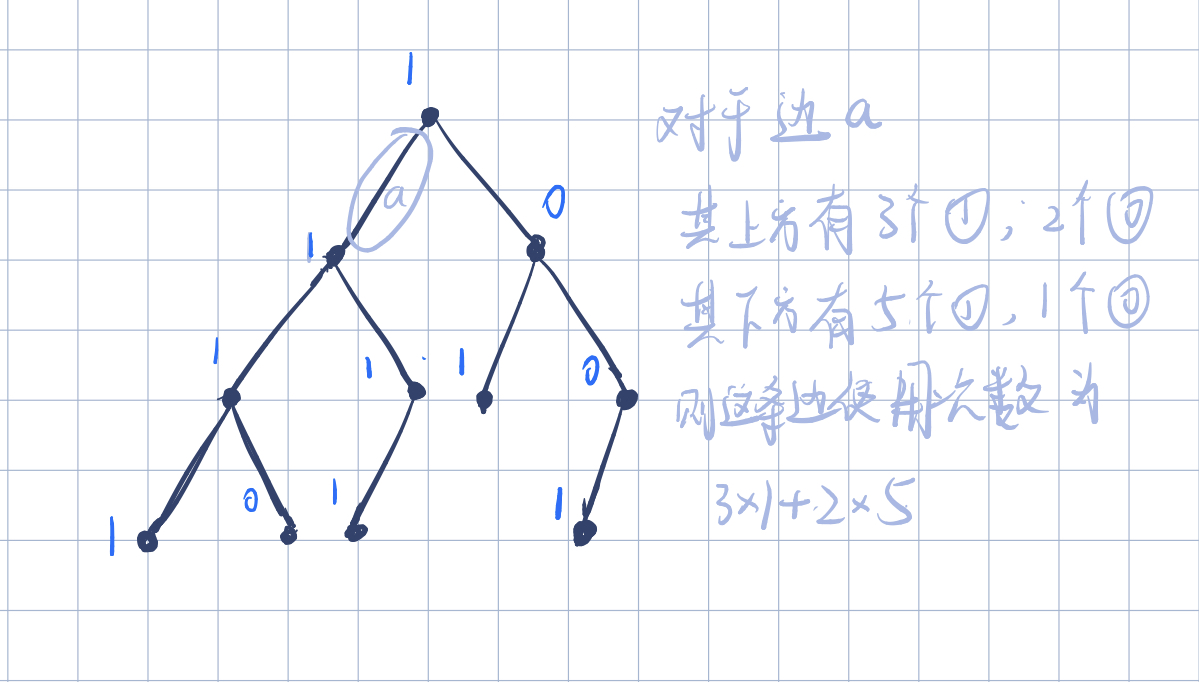
那么接下来的问题就转化为了如何得到这些数量,首先设这副图 0 的数量为 blcak , 1 的数量为 white ,那么只要保存这条边下方(也就是子树)的 0 的数量 nb,1 的数量 nw,那么答案就是 (black - nb)*nw + (white - nw)*nb,最后在乘以权值即可。那么我们就可以用dfs去求出其子树的 0 和 1 的数量。
代码:
1 #include<bits/stdc++.h> 2 #define ll long long 3 #define MOD 1000000007 4 #define INF 0x3f3f3f3f3f 5 #define mem(a,x) memset(a,x,sizeof(a)) 6 #define _for(i,a,b) for(int i=a; i< b; i++) 7 #define _rep(i,a,b) for(int i=a; i<=b; i++) 8 #define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); 9 10 using namespace std; 11 const int MAXN = 200005 ; 12 inline int rd() 13 { 14 int res = 0,flag = 0; 15 char ch; 16 if ((ch = getchar()) == '-')flag = 1; 17 else if(ch >= '0' && ch <= '9')res = ch - '0'; 18 while ((ch = getchar()) >= '0' && ch <= '9')res = (res<<1) + (res<<3) + (ch - '0'); 19 return flag ? -res : res; 20 } 21 // 22 int head[MAXN]; 23 int num=0; 24 struct edg{ 25 int next,to; 26 ll w; 27 }edge[MAXN]; 28 void edge_add(int u,int v,int w) //链式前向星存图 29 { 30 num++; 31 edge[num].next=head[u];edge[num].to=v;edge[num].w=w;head[u]=num; 32 edge[++num].next=head[v];edge[num].to=u;edge[num].w=w;head[v]=num; 33 } 34 int color[MAXN]; 35 vector<int>v; 36 struct node{ 37 int u,v; 38 ll w; 39 }s[MAXN]; 40 int fa[MAXN]; 41 int find(int x) 42 { 43 return (fa[x]==x)?x:(fa[x]=find(fa[x])); 44 } 45 void kruskal(int n,int m) 46 { 47 int nb=0; 48 for(int i=1;i<=m;i++){ 49 int fu=find(fa[s[i].u]),fv=find(fa[s[i].v]); 50 if(fu!=fv){ 51 fa[fu]=fv; 52 edge_add(s[i].u,s[i].v,s[i].w); 53 nb++; 54 v.push_back(s[i].w); 55 } 56 if(nb==n-1)break; 57 } 58 } 59 //////// 60 struct cc{ 61 int ww,bb; 62 }; 63 int mpw[MAXN]; 64 int mpb[MAXN]; 65 ll qpow(ll a,ll b) 66 { 67 ll ans=1; 68 while (b){ 69 if (b&1) ans=ans*a%MOD; 70 a=a*a%MOD; 71 b>>=1; 72 } 73 return ans; 74 } 75 cc dfs(int u,int fa) //求出任意边以下的白点和黑点数 76 { 77 cc col; 78 col.ww=0,col.bb=0; 79 for(int i=head[u];i!=-1;i=edge[i].next) 80 { 81 int v=edge[i].to; 82 if(v==fa)continue; 83 cc now=dfs(v,u); 84 col.ww+=now.ww; 85 col.bb+=now.bb; 86 mpw[edge[i].w]=now.ww; //读该边以下的白点数 87 mpb[edge[i].w]=now.bb; 88 } 89 cc p=col; 90 if(color[u]==1){ 91 p.ww++; 92 return p; 93 }else{ 94 p.bb++; 95 return p; 96 } 97 } 98 int main() 99 { 100 int T,n,m; 101 scanf("%d",&T); 102 while(T--){ 103 num=0; 104 v.clear(); 105 mem(head,-1); 106 int white=0,black=0; 107 scanf("%d %d",&n,&m); 108 for(int i=1;i<=n;i++){ 109 scanf("%d",&color[i]); 110 if(color[i]==1){ 111 white++; 112 }else{ 113 black++; 114 } 115 mpb[i]=0; 116 mpw[i]=0; 117 fa[i]=i; 118 } 119 for(int i=1;i<=m;i++){ 120 scanf("%d %d",&s[i].u,&s[i].v); 121 s[i].w=i; 122 } 123 kruskal(n,m); 124 dfs(1,0); 125 ll ans=0; 126 for(auto i:v) 127 { 128 int nw=white-mpw[i]; 129 int nb=black-mpb[i]; 130 ans=(ans+(1ll*nw*mpb[i]%MOD)*(qpow(2,i)%MOD))%MOD; 131 ans=(ans+(1ll*nb*mpw[i]%MOD)*(qpow(2,i)%MOD))%MOD; 132 } 133 printf("%lld ",ans); 134 } 135 return 0; 136 }