887. Super Egg Drop

问题：

给定K个鸡蛋，测试N层楼。

若鸡蛋在某一层落下后，刚好不摔碎（再上一层则摔碎），那么即检测到该层F为目标层。

问要检测到F层，最少测试次数为多少？

假设提供到F层被检测对象，为最坏结果（在某一层测试后，鸡蛋的碎或不碎状态，由使得测试对象要被测最多次来决定）

Example 1:
Input: K = 1, N = 2
Output: 2
Explanation: 
Drop the egg from floor 1.  If it breaks, we know with certainty that F = 0.
Otherwise, drop the egg from floor 2.  If it breaks, we know with certainty that F = 1.
If it didn't break, then we know with certainty F = 2.
Hence, we needed 2 moves in the worst case to know what F is with certainty.

Example 2:
Input: K = 2, N = 6
Output: 3

Example 3:
Input: K = 3, N = 14
Output: 4
 
Note:
1 <= K <= 100
1 <= N <= 10000

解法：

解法一：DP-1

DP(动态规划)+Binary Search(二分查找)

dp[k][n]：表示用k个鸡蛋测n层最少需要多少步。

动态转移方程：

dp[k][n] = min{ max(dp[k-1][i-1], dp[k][n-i]) + 1 } (1 <= i <= n)

推导过程：

我们要求【用k个鸡蛋测n层最少步数】

那么，我们需要【在所有策略中选择min步数的】

有哪些策略呢？

我们选择第 i 层去测试，刚好选择这一层，能得到最小测试步数，那么第 i 层则是我们要选择的对象。

因此，我们遍历0～N，所有层数，选取最小步数的

即：dp[k][n] = min((i:0~n)all case)

然后，对于第 i 层，我们去测试的时候，需要多少步呢？

这里，我们测试的话，会出现两种情况：

• 鸡蛋碎：
  • 我们损失一个鸡蛋，然后需要在这层的下方楼层中，选择一层进行下一次测试
  • 即：dp[k-1][i-1]
• 鸡蛋不碎：
  • 我们不损失鸡蛋，然后需要在这层的上方楼层中，选择一层进行下一次测试
  • 即：dp[k][n-i]

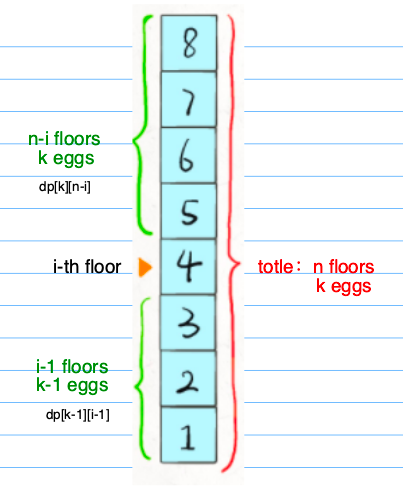
根据题意，我们面对的测试对象为最坏的情况，

鸡蛋碎或不碎，测试次数最多，符合题意。

因此操作次数为 max(dp[k-1][i-1], dp[k][n-i]) + 1

解释：碎或不碎的最大值+本次操作

边界情况：

• dp[0][n]：0个鸡蛋，n层楼：没法测试，测试步数为 0
• dp[1][n]：1个鸡蛋，n层楼：我们只能从第一层开始逐层向上测试，按题意最坏的结果则为测到最后一层楼，测试步数为 n
• dp[k][0]：k个鸡蛋，0层楼：不需要测试，测试步数为 0
• dp[k][1]：k个鸡蛋，1层楼：测一次即可，测试步数为 1

代码参考：

class Solution {
public:
    //dp[k][n]:k eggs, n floors->min moves to get result.
    //assume chose i-th floors to check
    //dp[k][n] = min((i:0~n)all case)
    //for i-th floor:
    //we have 2 possibilities: egg broken or nobroken
    //as the questions meaning, our test is the worst case,
    //which means, we have to face the max moves of the 2 possiblilities.
    //thus, max(broken, nobroken)
      //if broken:  we lost an egg, and should try next step in some floor under this floor(i-th floor)
                    // namely, dp[k-1][i-1]
      //if nobroken:we keep the same amount eggs, and should try next step in some floor above this floor
                    // namely, dp[k][n-i]
    //base case:
    //dp[0][n]:0  0 egg-> no moves to check. we can't check at all
    //dp[1][n]:n  1 egg-> we should check from 1st floor till the end. so the worst case is 'n'
    //dp[k][0]:0  0 floor-> no moves to check. there is no test object to check at all.
    //dp[k][1]:1  1 floor-> we need check one time at this 1st floor.
    int superEggDrop(int K, int N) {
        vector<vector<int>> dp(K+1, vector<int>(N+1,0));
        for(int n=0; n<=N; n++){
            dp[0][n] = 0;
            dp[1][n] = n;
        }
        for(int k=2; k<=K; k++){
            dp[k][0] = 0;
            dp[k][1] = 1;
        }
        for(int k = 2; k <= K; k++) {
            for(int n = 2; n <= N; n++) {
                dp[k][n] = INT_MAX;
                for(int i = 1; i <= n; i++) {
                    int broken = dp[k-1][i-1];
                    int nobroken = dp[k][n-i];
                    dp[k][n] = min(dp[k][n], max(broken, nobroken)+1);
                }
            }
        }
        return dp[K][N];
    }
};

这样直接使用DP的时间复杂度为 O(K * N^2)

会TLE（超时，Time Limit Exceeded）

因此，考虑优化♻️

观察动态转移方程

dp[n][k] = min{ max(dp[k-1][i-1], dp[k][n-i]) + 1 } (1 <= i <= n)

假设n和k为定值，那么根据方程含义，dp[k][i]

该函数应该为关于 i 的递增函数。

随着楼层的增大，测试步数也会增大。

而动态转移方程中，

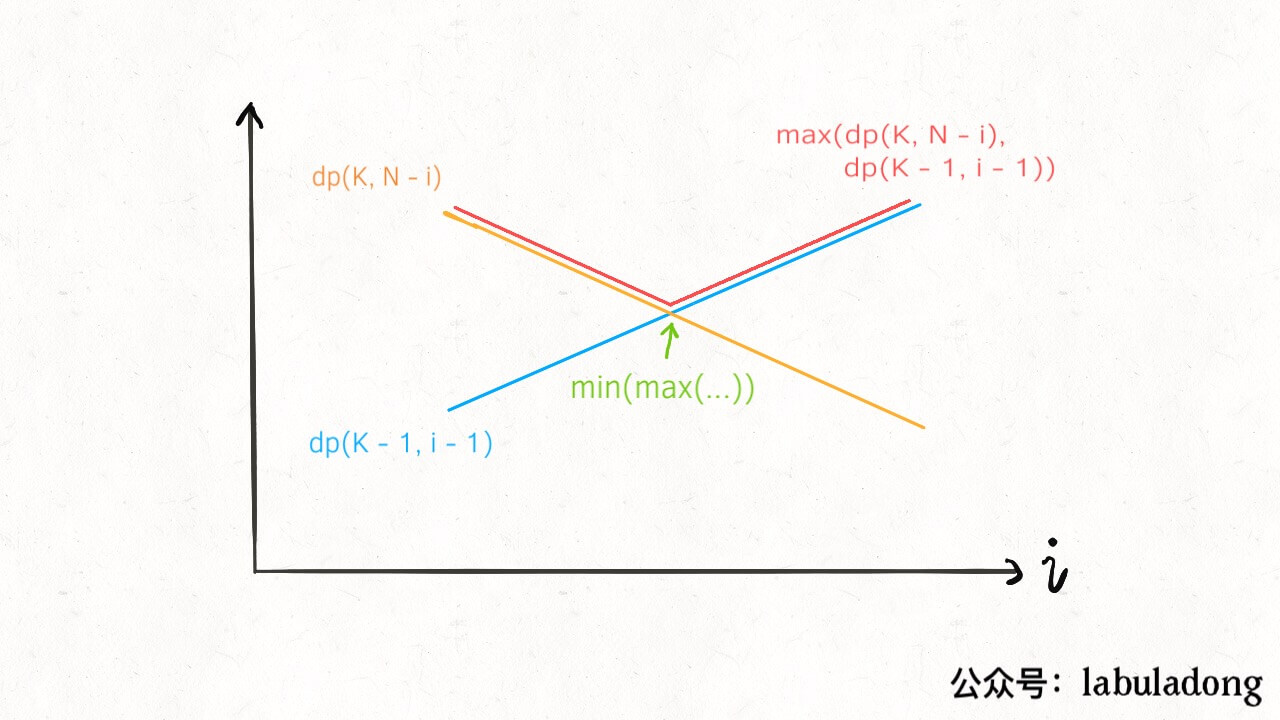
dp[k-1][i-1] 则为递增函数 broken

dp[k][n-i] 则为递减函数 nobroken

max(dp[k-1][i-1], dp[k][n-i]) 则为先减后增的函数

而要求的为min{ max(dp[k-1][i-1], dp[k][n-i]) + 1 }，则为最低点。

这里，我们可以使用二分查找，找到最低点，

找第一个使得 broken >= nobroken 的 i

 代码参考：

class Solution {
public:
    int superEggDrop(int K, int N) {
        vector<vector<int>> dp(K+1, vector<int>(N+1,0));
        for(int n=0; n<=N; n++){
            dp[0][n] = 0;
            dp[1][n] = n;
        }
        for(int k=2; k<=K; k++){
            dp[k][0] = 0;
            dp[k][1] = 1;
        }
        for(int k = 2; k <= K; k++) {
            for(int n = 2; n <= N; n++) {
                dp[k][n] = INT_MAX;
                int l=1, r=n+1;
                while(l<r){
                    int mid = l+(r-l)/2;
                    int broken = dp[k-1][mid-1];
                    int nobroken = dp[k][n-mid];
                    if(broken>=nobroken){
                        r = mid;
                    } else {
                        l = mid+1;
                    }
                }
                dp[k][n] = dp[k-1][l-1]+1;
                /*for(int i = 1; i <= n; i++) {
                    int broken = dp[k-1][i-1];
                    int nobroken = dp[k][n-i];
                    dp[k][n] = min(dp[k][n], max(broken, nobroken)+1);
                }*/
            }
        }
        return dp[K][N];
    }
};

---

解法二：DP-2

DP(动态规划)

dp[k][m]=N：表示用k个鸡蛋测m步，最多能测多少层。

最后要求的m，满足dp[k][m]>=N即可。

动态转移方程：

dp[k][m] = dp[k-1][m-1] + dp[k][m-1] + 1

推导过程：

我们要求【用k个鸡蛋测m步，最多能测的层数】

我们在任意一次测试，会出现两种情况：

• 鸡蛋碎：
  • 我们损失一个鸡蛋，损失一步操作，下一步在本楼以下楼层进行测试
  • 最多用k-1个鸡蛋，m-1步，能测dp[k-1][m-1]层楼。
• 鸡蛋不碎：
  • 我们不损失鸡蛋，损失一步操作，下一步在本楼以上楼层进行测试
  • 最多用k个鸡蛋，m-1步，能测dp[k][m-1]层楼。

 对于本层，我们能测的最多层数：本层之上的可能层数dp[k][m-1]+本层之下的可能层数dp[k-1][m-1]+本层 1

这里，【最坏情况】为固定层数，测试的步数最大，

dp[k][n]：dp[1蛋][7层]=7步，线性从第一次逐次向上试。

dp[k][m]：dp[1蛋][7步]=7层，=dp[0][6]+dp[1][6]+1=0+6+1...dp[1][1]=dp[0][0]+dp[1][0]+1=1，刚好是满足【最坏情况】的。 

边界情况：

• dp[0][m]：0个鸡蛋，m步测试：没法测试，测试层数为 0
• dp[k][0]：k个鸡蛋，0步测试：不需要测试，测试层数为 0

代码参考：

class Solution {
public:
    //dp[k][m]:k eggs, try m times, can determine the max height of floors.
    //assume chose i-th floors to check
    //total height = current height + the max height of under floors + the max height of above floors
    //dp[k][m] = 1 + dp(if boken) + dp(if nobroken)
      //if broken:  we lost an egg, and lost one challenge chance
                    // namely, dp[k-1][m-1]
      //if nobroken:we keep the same amount eggs, and lost one challenge chance
                    // namely, dp[k][m-1]
    //base case:
    //dp[0][m]:0  0 egg-> we can't check at all. thus max floors = 0
    //dp[k][0]:0  0 moves-> no moves to check. thus max floors = 0.
    int superEggDrop(int K, int N) {
        vector<vector<int>> dp(K+1, vector<int>(N+1,0));
        int k=0, m=0;
        while(dp[K][m]<N) {
            m++;
            for(k=1; k<=K; k++) {
                dp[k][m] = 1 + dp[k][m-1] + dp[k-1][m-1];
            }
        }
        return m;
    }
};

♻️ 优化：

将二维DP化为一维DP

dp[k][m] = dp[k-1][m-1] + dp[k][m-1] + 1

去掉m

dp[k] = dp[k-1] + dp[k] + 1

-> dp[k] += dp[k-1]+1

映射二维k，m到一维 k

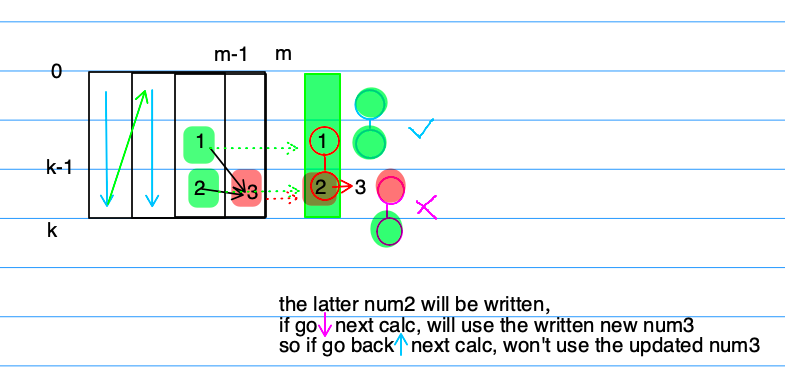
考虑三个变量的更新情况，如下图

需要将k的遍历，改为从下向上 ↑ 倒向遍历，才不会影响赋值情况。

 代码参考：

class Solution {
public:
    int superEggDrop(int K, int N) {
        vector<int> dp(K+1,0);
        int k=0, m=0;
        while(dp[K]<N) {
            m++;
            for(k=K; k>0; k--) {
                dp[k] += 1 + dp[k-1];
            }
        }
        return m;
    }
};

DP-2

的参考解释：

https://leetcode.com/problems/super-egg-drop/discuss/158974/C%2B%2BJavaPython-2D-and-1D-DP-O(KlogN)

Sandermatt74         Last Edit: October 27, 2018 5:42 AM

He has turned the problem around from
"How many moves do you need to check N floors if you have K eggs"
to:
"How many floors can you check given M moves available and K eggs".

If you can solve this second problem than you can just increase the moves M one by one until you are able to check a number of floors larger or equal to the number N which the problem requires.
He then defined
dp[M][K] as the maximum number of floors that you can check within M moves given K eggs

A move essentially is dropping an egg and it either breaks or doesn't break.
Case A: The egg breaks and now you have spent 1 move (M=M-1) and also lost 1 egg (K=K-1). You can still check dp[M-1][K-1] floors, with your remaining eggs and moves.
Case B: The egg remains and you only loose one move (M=M-1). You can still check dp[M-1][K] floors.
Additionally you just checked a floor by dropping the egg from it.
Therefore dp[M][K] = dp[M - 1][k - 1] + dp[M - 1][K] + 1
As you can see we can easily calculate how many floors we can check in M moves if we know how many floors we can check in M-1 moves.

However we not only have to know how many floors we can can check with one move less, but also how many we can check with one move and one egg less. Therefore we have to calculate how many moves we can check for all number off eggs from 1 to K.

An example:
N = 6 and K = 2
Turn the problem around: How many floors can you check with 2 eggs and M moves:

Solve for M=1, K=1,2
you can only check 1 floor (since afterwards you have no more moves left)

Solve for M=2, K=1
Case A: Your egg breaks, you have no more eggs left and can check nothing. dp[M=1,K=0]=0
Case B: your egg survives and you can use it to test an additional floor above the floor you just tested. dp[M=1,K=1]=1
dp[2][1]=dp[1][0]+dp[1][1]+1=0+1+1=2

Solve for M=2, K=2
Case A: Your egg breaks: you have 1 move left and 1 egg. Since you know that the floor F where the eggs break is below the floor you just tested you can now check dp[M=1,K=1] floors below you, with only 1 move left you check 1 additional floor below. dp[M=1,K=1]=1
Case B: Your eggs survives and you start to search above the current floor. dp[1][2] is still only 1 move and we can check 1 floor. dp[1][2]
dp[2][2]=1+1+1=3

Solve for M=3, K=1
Case A: Your egg breaks and you are out of eggs, no chance to check anything anymore
Case B: Your egg survives and you can use it for 2 more moves dp[2][1], which as we established above is enough to check 2 floors.
dp[3][1]=0+2+1=3

Solve for M=3, K=2
Case A: Your egg breaks and you check dp[2][1]=2 additional floors
Case B: Your egg survives and you check dp[2][2]=3 additional floors
dp[3][2]=2+3+1=6

As you can see 3 moves and 2 eggs allows you to check 6 floors. Which answers the original question how many moves you need to check 6 floors given 2 eggs,
The answer is 3

I hope this helps to make it more clear.