问题:
给定一棵树,root=0
每个节点id有值nums[id]
求每个节点的所有祖先中,最近&&与其值互质的父节点。
Example 1: Input: nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]] Output: [-1,0,0,1] Explanation: In the above figure, each node's value is in parentheses. - Node 0 has no coprime ancestors. - Node 1 has only one ancestor, node 0. Their values are coprime (gcd(2,3) == 1). - Node 2 has two ancestors, nodes 1 and 0. Node 1's value is not coprime (gcd(3,3) == 3), but node 0's value is (gcd(2,3) == 1), so node 0 is the closest valid ancestor. - Node 3 has two ancestors, nodes 1 and 0. It is coprime with node 1 (gcd(3,2) == 1), so node 1 is its closest valid ancestor. Example 2: Input: nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]] Output: [-1,0,-1,0,0,0,-1] Constraints: nums.length == n 1 <= nums[i] <= 50 1 <= n <= 105 edges.length == n - 1 edges[j].length == 2 0 <= uj, vj < n uj != vj
example 1:
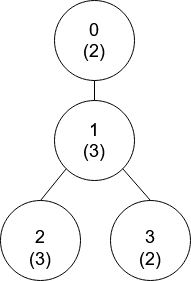
example 2:
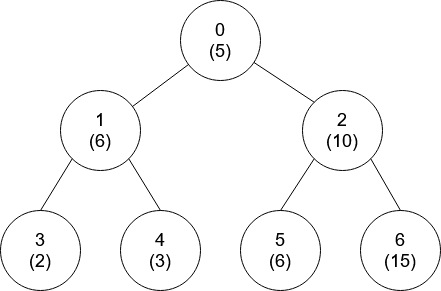
解法:DFS
思路:
- 对树进行深度优先遍历DFS,那么每次遍历出来的一条线:即是一条继承线。使用ancestor进行记录。
- 对于每个当前的节点 i
- 我们需要找到其祖先ancestor中,与他互质的祖先们,
- 然后在这些祖先中,找到level最大,即离 i 最近。
- 那么我们先构造互质关系cops
- 值 i,的互质数有 {值a,值b,值c...}
- cops[i] = {a,b,c...}
- 这样一个unordered_map
⚠️ 注意:由于构造是以数值为基础,那么我们为了不重复计算,使用unordered_set,将所有nums过滤出来,再进行构造。
- 对于当前节点 i,值为 nums[i]
- 找到这个值的所有互质数,cops[nums[i]]
- 对于其中一个互质数,onecop in cops[nums[i]]
- 祖先中存在这个数onecop,ancestor[onecop]是所有值为onecop的祖先(可能有多个值相同的祖先)
- 取最后一个祖先,一定是最后加入ancestor的,也是离 i 最近&&值为onecop的祖先。
- 同样的,找到所有不同互质祖先的最近者,在这些不同值的祖先中,再取最近的祖先。
- 即为所求。
对于DFS
- 状态:
- 当前node:i,值 nums[i]
- 当前层次:level
- 到目前为止的继承线: ancestor
- 选择:
- i 的所有子节点(所有相邻节点-父节点)
参考辅助信息:
- 结果:res:各个节点的结果
- 节点的相邻关系:graph:
- 节点 i 的相邻节点有{a,b,c...},则graph[i]={a,b,c...}
- 同时graph[a],graph[b],graph[c]也都分别含有 i。
- 节点 i 的相邻节点有{a,b,c...},则graph[i]={a,b,c...}
- 互质数关系:cops
- 值 i,的互质数有 {值a,值b,值c...},则cops[i] = {a,b,c...}
代码参考:
1 class Solution { 2 public: 3 //dfs: 4 //记录一条继承关系下来的所有节点。ancestor:map: key:数值, vector<value>:层次+id 5 //对于当前节点 i 6 //在其ancestor中, 7 //对所有与num[i]互质的数值cop(list)中,找离他最近的祖先。 8 // 对于同一个互质数cop[j], 离他最近的祖先:即是,最后一个加入ancestor的数。 9 // 然后,对所有互质数,求最近的ancestor。 10 //状态:节点id: i, 节点值: num[i] 11 // 层次: level, 12 // 这一路的继承带:ancestor 13 //选择:所有相邻节点-**父节点** 14 unordered_map<int,vector<int>> cops;// key:num[i], value:{与key互质的所有数} 15 unordered_map<int,vector<pair<int, int>>> ancestor; 16 vector<vector<int>> graph; 17 void dfs(vector<int>& res, vector<int>& nums, 18 int i, int level,//state 19 int parent) {//options 20 // for current node i 21 auto nearst_level = -1;//level 22 for(int onecop:cops[nums[i]]) {//for all 节点i的互质数 23 //for 祖先value=onecop 的所有祖先 24 if(ancestor[onecop].empty()) continue;//没有这样互质的祖先 25 auto [acst_level, acst_id] = ancestor[onecop].back();//有这个互质祖先,取最近 26 if(acst_level>nearst_level) {//各种互质数之间,有更近的,更新结果为最新的。 27 nearst_level = acst_level; 28 res[i] = acst_id; 29 } 30 } 31 //将当前节点加入祖先 32 ancestor[nums[i]].push_back({level, i}); 33 //选择:所有孩子 34 for(int child:graph[i]) { 35 if(child==parent) continue; 36 dfs(res, nums, child, level+1, i); 37 } 38 //将当前节点弹出 39 ancestor[nums[i]].pop_back(); 40 return; 41 } 42 vector<int> getCoprimes(vector<int>& nums, vector<vector<int>>& edges) { 43 unordered_set<int> s(begin(nums), end(nums)); 44 vector<int> res(nums.size(),-1); 45 graph.resize(nums.size()); 46 //create 互质 info 47 for(int i:s) { 48 for(int j:s) { 49 if(__gcd(i,j)==1) cops[i].push_back(j); 50 } 51 } 52 //create graph 53 for(auto ed:edges) { 54 graph[ed[0]].push_back(ed[1]); 55 graph[ed[1]].push_back(ed[0]); 56 } 57 dfs(res, nums, 0, 0, 0); 58 return res; 59 } 60 };