The sum of arithmetic sequence
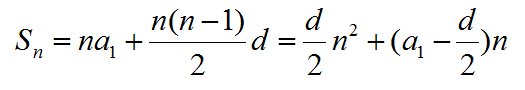
The sum of geometric sequence
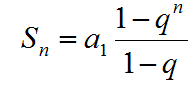
A special formula : n·n! = (n+1)! - n!
Divisible Test
4: The last 2 digits are divisible by 4
6: Divisible by both 2 and 3
7: Truncate the final digit. Use the rest minus the final digit truncated twice. Check the answer if can be divisible by 7. [ truncation, double, distraction, check ]
8: The last 3 digits are divisible by 8
9: Sum of digits is divisible by 9
11: Add and subtract digits alternating from left to right. Check the answer if can be divisible by 11
913 ( 9 - 1 + 3 = 11 yes )
1364 ( 1 - 3 + 6 - 4 = 0 yes )
987 ( 9 - 8 + 7 = 8 no )
3729 ( 3 - 7 + 2 - 9 = -11 )
The number of divisors
72 = 23 x 32
( 3 + 1 ) x ( 2 + 1 ) = 12
Each exponent plus one and multiply together
The factor of polynomial
a1xn + a2xn-1 + ······ + anx + k = 0
if it can divide by ( x - s ) , then s is a factor of k/a1
a3 - 8a + 8 = 0
8/1 = 8 → ±1, ±2, ±4, ±8
Vieta's theorem
ax3 + bx2 + cx + d = 0
x1 + x2 + x3 = -b/a
x1x2 + x1x3 + x2x3 = c/a
x1x2x3 = -d/a
Entire radical : the coefficient is one 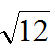
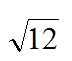
Mixed radical : 
f(x) ÷ (x-a) = quotient ······ f(a)
if f(a) = 0, f(x) is divisible by (x-a)
Ex.1. What's the remainder of (5x3 + 4x2 - 12x + 1) ÷ (x - 3)
5·33+4·32-12·3+1=136
Ex.2. What's the remainder of (x4+x) ÷ (x2-3x+2)
let ax+b be the remainder ( the degree of remainder is less 1 than divisor's )
Solve the divisor, x=1,2
(14+1) = a·1+b
(24+2) = a·2 +b
→ a=16, b=-14
therefore the remainder is 16x-14
Theorem about Secant, Tangent and Arc
