1. 题目
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
2. 示例

示例1:
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例2:
输入:n = 1
输出:[["Q"]]
3. 题解
首先看下约束条件:
1. 不能同行
2. 不能同列
3. 不能同斜线
确定完约束条件,来看看究竟要怎么去搜索皇后们的位置,其实搜索皇后的位置,可以抽象为一棵树。
下面我用一个3 * 3 的***,将搜索过程抽象为一颗树,如图:
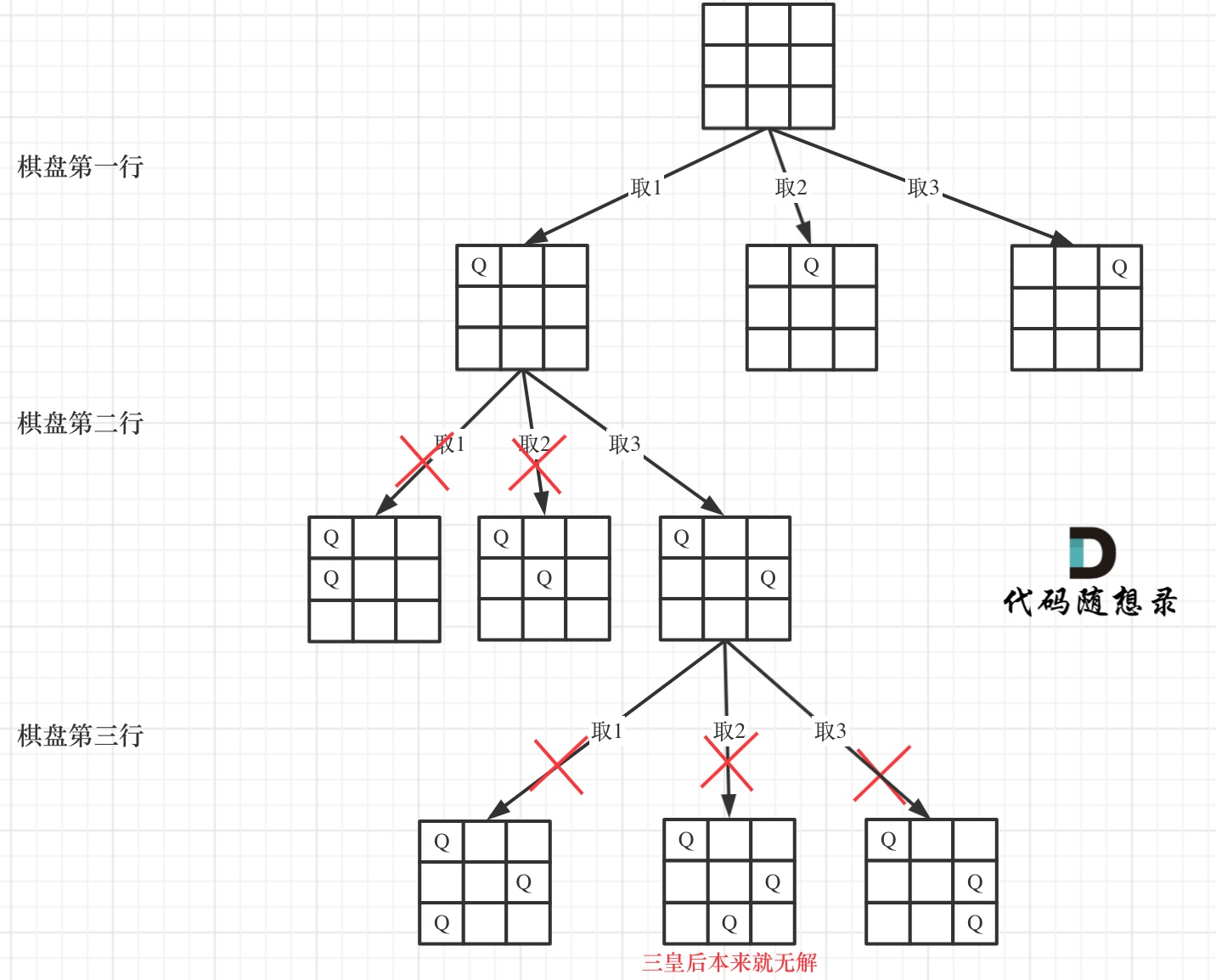
图中,可以看出,二维矩阵中矩阵的高就是这颗树的高度,矩阵的宽就是树形结构中每一个节点的宽度。
那么我们用皇后们的约束条件,来回溯搜索这颗树,只要搜索到了树的叶子节点,说明就找到了皇后们的合理位置了。
接下来回溯三部曲:
回溯总模板:
result = []
def backtrack(路径,选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径,选择列表)
撤销选择
1. 路径
res = []
board = [['.'] * n for _ in range(n)]
2. 选择列表
行与列作为选择列表
for col in range(n):
# 排除不合法选择
if not self.isValid(board, row, col):
continue
# 做选择
board[row][col] = 'Q'
# 进入下一行决策
backtrack(board, row + 1, n)
board[row][col] = '.'
3. 结束条件
# 触发条件
if row == n:
temp_res = []
for temp in board:
temp_str = "".join(temp)
temp_res.append(temp_str)
res.append(temp_res)
return
4. 完整代码实现
1 class Solution:
2 def isValid(self, board, row, col):
3 n = len(board[row])
4 # 检查列中是否有皇后相互冲突
5 for i in range(n):
6 if board[i][col] == 'Q':
7 return False
8 # 检查左上方是由有皇后相互冲突
9 i, j = row - 1, col - 1
10 while i >= 0 and j >= 0:
11 if board[i][j] == 'Q':
12 return False
13 i -= 1
14 j -= 1
15 # 检查右上方是否有皇后互相冲突
16 i, j = row - 1, col + 1
17 while i >= 0 and j < n:
18 if board[i][j] == 'Q':
19 return False
20 i -= 1
21 j += 1
22 return True
23
24 def solveNQueens(self, n: int) -> List[List[str]]:
25 res = []
26 board = [['.'] * n for _ in range(n)]
27
28 def backtrack(board, row, n):
29 # 触发条件
30 if row == n:
31 temp_res = []
32 for temp in board:
33 temp_str = "".join(temp)
34 temp_res.append(temp_str)
35 res.append(temp_res)
36 return
37 for col in range(n):
38 # 排除不合法选择
39 if not self.isValid(board, row, col):
40 continue
41 # 做选择
42 board[row][col] = 'Q'
43 # 进入下一行决策
44 backtrack(board, row + 1, n)
45 board[row][col] = '.'
46
47 backtrack(board, 0, n)
48 return res
5. 结语
努力去爱周围的每一个人,付出,不一定有收获,但是不付出就一定没有收获! 给街头卖艺的人零钱,不和深夜还在摆摊的小贩讨价还价。愿我的博客对你有所帮助(*^▽^*)(*^▽^*)!
如果客官喜欢小生的园子,记得关注小生哟,小生会持续更新(#^.^#)(#^.^#)。