1、三和弦
上一篇作为准备介绍了音程,在最后介绍了纯四度和纯五度循环与半音循环的同构性。在我们刚刚开始生成和弦的时候,大家请明确一个事实性的结论:除了一度和八度,纯四度和纯五度是听上去最为和谐的音程。
和声(Harmony)的意义就在于令声音听上去和谐,而和弦(Chord)是和声理论的重点。古典理论中“和弦”只是指三个及以上的音以三度关系叠加起来的结构,而现代理论并不拘泥于此。为什么是三度、三个音比较难以解释,但确实是比较简单的情况。很有趣的是,上文提到过的具有循环结构的减七和弦、增三和弦、小六度等,听上去是非常不和谐的。下面我们从简单而和谐的和弦开始。
我们来尝试产生最基本的三和弦。为了通过三度叠加得到纯五度音程,我们很容易就发现这样一种方式:大三度 + 小三度 = 纯五度,也就是$4+3=7$。这种方式就是最传统的大三和弦。
C — E — G就是一个大三和弦。C在其中称为根音,E称为三音,G称为五音。请注意如果调换位置成为E — G — C,虽然还是大三和弦,但G — C不是三度音程,不能把E当作根音。尝试听,大三和弦的听觉效果是明亮的。
不同的根音可以生成的大三和弦总共有12个。譬如C — E — G,然后继续生成:G — B — D,……。如果画成图就像下面这样(只标出了#号):
可以看到生成了全部的12个大三和弦。请注意其中有一些为了音名的清晰性并没有标成三度,比如C# — F — G#,三音标成E#更为合适。
大三和弦的简记可以直接用根音代替,譬如C表示C — E — G。当然有时也用Cmaj等记号,目前没有明确的说法。
上面的图把大三和弦表达成了正放的三角形。观察其中自然出现的倒三角形,可以看到它们都具有小三度 + 大三度 = 纯五度的结构,也即除大三和弦外另一种非常重要而基础的和弦:小三和弦。它来自于$3+4=7$这样一个简单的事实。同样,小三和弦也有根音、三音、五音的说法。尝试听,小三和弦的听觉效果是忧郁的。
在上图中画出小三和弦,就像这样:
小三和弦的记法就加上m,例如Cm。
如果我们观察同一个根音的大三和弦和小三和弦,譬如:C — E — G和C — Eb — G,可以发现它们只有三音是不同的,可是听觉效果却完全不一样。这是一个非常重要的性质,它表明,在根音确定的情况下,三音是三和弦的决定音。五音有时显得不那么重要,主要是因为它无法构成“色彩”(一个比较模糊的概念)。但根音和五音也可以组成强力和弦等有重要应用的和弦,这些之后再说。
大三和弦和小三和弦之间有明确的周期关系。如果大家有键盘乐器(或者App),可以尝试这样做:弹出一个大三和弦,这是一个$4+3$,然后以这个和弦的$3$为基础,弹出下一个小三和弦$3+4$,反复进行,直到遍历了24个基础三和弦为止。当然,更清晰的周期关系是把上面画出来的三角形并到一起: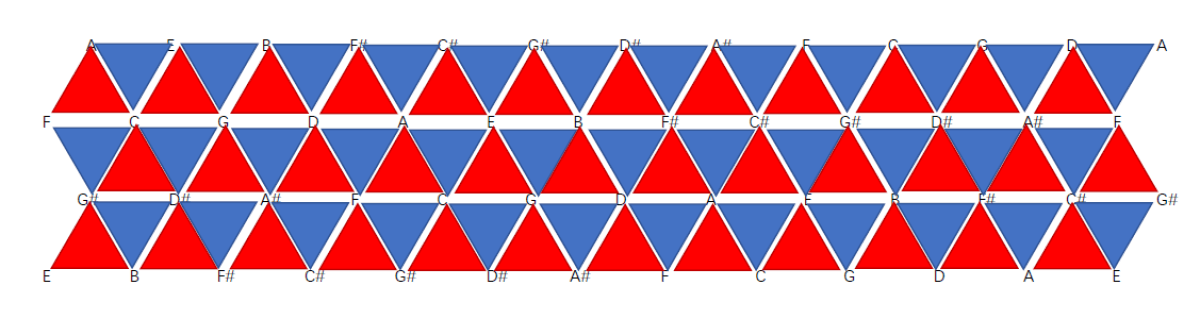
这张图(三和弦网格图)此前我也没有听说过,来自于《图解和声》,据说是欧拉率先发现的。可以看出这是一个可以无限密铺下去的图。这张图有一些非常重要的性质,这里我们先介绍几个:
1、正放的三角形就是大三和弦,倒放的就是小三和弦。我们就是这样生成这张图的。
2、每条横线,向右进行就是纯五度循环,向左进行就是纯四度循环。其实来源于三和弦的根音和五音之间的音程关系。
3、向右上方进行就是大三度循环,向右下方进行就是小三度循环。这是因为我们把三和弦的三音摆在了三角形的上顶点的位置。
4、每条竖线都是一个半音阶循环。
其它的性质我们此后再说。网络上难以找到这张图,因此我将其画了出来。如果大家有这个工具,不需要键盘、五线谱我想也能理解我们提到的和声知识,而且重要的是这张图的平铺周期性质可以帮助我们很好地规避“C调依赖症”。大家最好拥有这张图,甚至会画。